Capitolo 8 - Cartografia

8.1       Introduzione alle carte.

In molte delle nostre attività, scientifiche e pratiche, accanto all'esigenza primaria di un esame diretto dell'oggetto di cui ci stiamo occupando, sentiamo spesso la necessità di avere a disposizione una sua immagine o una sua rappresentazione grafica: insomma, ci serve un modello che consenta una visione di insieme sufficientemente dettagliata e precisa, anche se in dimensioni ridotte, dell'oggetto di nostro interesse e dei suoi vari aspetti; un modello sul quale si possono anche annotare i dati di maggiore importanza per l'attività che stiamo effettuando.

Osservando alcune delle stupende fotografie scattate dai satelliti in orbita, abbiamo potuto dare uno sguardo di insieme al nostro pianeta; fotografie di porzioni ristrette della superficie terrestre vengono frequentemente eseguite, da aerei in volo a quote che possono variare da alcune centinaia ad alcune migliaia di piedi.

Il telerilevamento è di indubbia utilità nello studio del nostro pianeta e per la stessa costruzione delle Carte geografiche; queste ultime comunque rimangono uno strumento indispensabile per ogni serio esame della superficie terrestre e dei suoi vari aspetti.

8.2       I globi e le Carte geografiche.

Come è noto, la Terra ha una forma sferoidale, e quindi può essere rappresentata con una certa precisione solo tramite una superficie sferica, ossia utilizzando un globo; effettivamente solo un globo può essere definito come la fedele riproduzione in piccolo della Terra (Figura 8.3).

Naturalmente, date le dimensioni ridotte, sui globi possono essere riportati soltanto i tratti generali del nostro pianeta e questi dovranno essere contrassegnati da simboli particolari che siano in grado di ricordarci ciò che rappresentano.

Oltre ad essere costosi e poco maneggevoli, i globi, a causa delle loro dimensioni necessariamente limitate non ci consentono di raffigurare la superficie terrestre con quella ricchezza di particolari che tanto spesso è assolutamente necessaria per gli scopi pratici.

La Carta inoltre è approssimata, ossia non è rigorosamente esatta, poiché non è possibile sviluppare su un piano una superficie sferica come e quella della Terra senza che essa subisca delle deformazioni (Figura 8.5).

I metodi utilizzati per rappresentare in piano la superficie terrestre costituiscono le proiezioni geografiche. Gli oggetti geografici (siano essi particolarità del terreno, opere umane ecc.) dovranno essere indicati tramite simboli particolari, detti segni convenzionali, i quali ci ricordino in qualche modo gli elementi rappresentati: una Carta geografica perciò è anche simbolica.

Affinché una qualsiasi rappresentazione della Terra possa essere considerata esatta, deve presentare contemporaneamente tre requisiti:

• l'equidistanza (cioè si deve mantenere inalterato il rapporto tra le lunghezze grafiche e le lunghezze reali che esse rappresentano);
• l'equivalenza (ossia deve essere costante il rapporto tra le aree grafiche e le corrispondenti aree reali);
• l'isogonia (cioè l'angolo formato tra due linee qualsiasi che compaiono nella rappresentazione deve essere uguale all'angolo compreso tra le corrispondenti linee sulla superficie terrestre).

Le Carte che posseggono questi requisiti sono dette rispettivamente: equidistanti, equivalenti e isogone (o conformi).

Da quanto detto, appare chiaro però che soltanto i globi possiedono contemporaneamente i tre requisiti suddetti; le Carte geografiche, essendo approssimate, potranno rispettare al massimo uno di tali requisiti e generalmente nemmeno in modo completo: ad esempio, se sono equidistanti non lo sono in tutte le direzioni.

Comunque, si può affermare che se le zone rappresentate sono molto ristrette le moderne Carte geografiche sono considerabili, in pratica, come graficamente esatte.

8.3       La Scala delle Carte geografiche.

Si è già detto che non si può riprodurre la superficie terrestre in grandezza naturale, ma che è necessaria una riduzione secondo un determinato rapporto, detto Scala.

In particolare, si definisce Scala numerica (lineare) di una Carta geografica il rapporto tra una lunghezza misurata sulla Carta e la corrispondente lunghezza sulla superficie terrestre.

Tale rapporto è espresso sotto forma di una frazione (1:N) in cui il numeratore rappresenta l'unità ed il denominatore N esprime il numero di volte di cui le distanze reali sono state ridotte sulla Carta. Così, ad esempio, "Scala 1:100.000" (che si legge: "Scala uno a centomila") vuol dire che ad una certa lunghezza misurata sulla Carta corrispondono 100.000 di tali lunghezze sul terreno; cioè, in pratica, 1 mm sulla Carta = 100.000 mm (ossia 100 m) sul terreno, 1 cm sulla Carta = 100.000 cm (ossia 1 Km) sul terreno, e cosi via.

Dato che questo rapporto è espresso sotto forma di frazione, è evidente che la Scala di una Carta geografica sarà tanto più grande quanto più piccolo è il denominatore, e viceversa. Ne segue che potremo chiamare "Carte a grande Scala" quelle per le quali il valore di N e piccolo (di solito inferiore a 150.000) e "Carte a piccola Scala" quelle in cui N e grande (in genere maggiore di 150.000).

Tenendo presente ciò, è anche chiaro che la Scala 1:25.000 è doppia della Scala 1:50.000, essendo 1:25.000 = 2 x (1:50.000); così la Scala 1:10.000 è doppia di quella 1:20.000, mentre è tre volte più grande di quella 1:30.000, quattro volte maggiore di quella 1:40.000 ecc.

Oltre alla Scala numerica, sulle Carte è riportata spesso anche la Scala grafica, cioè la rappresentazione grafica del rapporto numerico di riduzione (Figura 8.6). Si tratta di due segmenti paralleli divisi in tanti tratti uguali, detti unità grafiche, che corrispondono a determinate lunghezze sul terreno (in metri, kilometri, miglia ecc.) ed i cui valori vengono riportati su ogni divisione.

8.4       Classificazione delle Carte geografiche.

Le Carte geografiche possono essere classificate sia in base alla Scala di riduzione, sia in base al loro contenuto, sia in base al metodo con cui vengono costruite.

Rispetto alla Scala distinguiamo quattro gruppi di Carte.

           Piante e mappe, aventi una Scala maggiore di 1:10.000.

Sono Carte molto dettagliate, e rappresentano con estrema ricchezza di particolari zone limitate.

Le piante raffigurano la planimetria dei centri urbani, mentre le mappe sono utilizzate essenzialmente per rappresentare le proprietà rurali (poderi, zone boscose, pascoli ecc.).

           Carte topografiche, con una Scala compresa fra 1:10.000 è 1:150.000. Anche queste Carte sono piuttosto particolareggiate e rappresentano piccoli tratti di superficie terrestre, dei quali evidenziano sia le fattezze naturali sia le opere umane. Queste Carte vengono rilevate nei vari paesi da appositi enti e servono per la costruzione delle Carte a Scala minore; perciò sono dette anche Carte di base.

           Carte corografiche, aventi Scala variabile da 1:150.000 a 1:1.000.000. Esse raffigurano zone abbastanza estese della Terra con un discreto numero di particolari (specialmente le vie di comunicazione) e possono rappresentare una intera regione.

           Carte geografiche propriamente dette, nelle quali la Scala è minore di 1:1.000.000.

Esse rappresentano aree molto estese della superficie terrestre, come, ad esempio, uno o più stati o addirittura un intero continente. A tale gruppo appartengono anche i mappamondi (rappresentazione in piano della Terra, divisa in due emisferi) ed i planisferi (rappresentazione in piano di tutta la Terra, la cui Scala non è mai superiore a 1:30.000.000).

In base al contenuto, vengono solitamente distinte le Carte generali (o normali), le Carte speciali e le Carte tematiche.

           Nelle Carte generali sono rappresentate o le sole fattezze naturali, quali i fiumi, i laghi, le coste ecc. (Carte fisiche) o gli aspetti umani, cioè i confini politici ed amministrativi, le città, le strade, le ferrovie ecc. (Carte politiche), oppure entrambi i suddetti elementi (Carte fisico-politiche).

           Le Carte speciali, sono costruite per uno scopo preciso e richiedono generalmente un particolare tipo di proiezione. Tra queste meritano di essere citate soprattutto: le Carte idrografiche, che comprendono le Carte marine, in cui sono rappresentati i mari e le coste, le Carte nautiche, necessarie alla Navigazione marittima le Carte idrografiche continentali relative alle acque (fiumi, laghi) distribuite sulle terre emerse, le Carte aeronautiche, usate per la Navigazione aerea.

           Le Carte tematiche, mettono in risalto particolari aspetti fisici, biologici, antropici ed economici. Così ad esempio, si hanno le Carte geomorfologiche, che rappresentano le forme del terreno e la loro genesi; le Carte climatiche, relative alla distribuzione dei diversi tipi climatici; le Carte della vegetazione, che indicano il tipo di copertura vegetale presente nella porzione di superficie terrestre raffigurata; le Carte antropologiche ed etnologiche, che visualizzano la distribuzione delle popolazioni e delle lingue e religioni le Carte economiche, che rappresentano la distribuzione ed i caratteri dei fatti economici connessi con le attività umane (materie prime, allevamenti, produzioni agricole, industrie, vie di comunicazione, commerci ecc.).

In base al metodo di costruzione, le Carte geografiche possono essere distinte in Carte rilevate e Carte derivate.

           Le Carte rilevate sono costruite e disegnate basandosi su misure ed osservazioni dirette eseguite sul terreno.

           Le Carte derivate si ottengono dalle precedenti tramite semplificazioni e riduzioni (onde il norme di derivate).

8.5       Le proiezioni geografiche

I vari sistemi elaborati per riportare sul piano il reticolato geografico, che costituisce la base di una Carta, cioè la trama su cui raffigurare gli elementi della superficie terrestre, prendono il nome di proiezioni geografiche; queste possono essere fondate su procedimenti geometrici o matematici e vengono scelte in base alla finalità della Carta e secondo il numero degli oggetti reali che su di essa si vogliono poi riportare.

Sostanzialmente le proiezioni geografiche si dividono in proiezioni pure, modificate e convenzionali.

           Nelle proiezioni pure il reticolato geografico viene riportato su di una superficie ausiliaria, applicando i soli principi geometrici. Detta superficie può essere un piano (proiezioni prospettiche) o quella di un solido sviluppabile in piano (proiezioni di sviluppo).

           Le proiezioni modificate si ottengono dalle precedenti, apportando alla costruzione geometrica quelle correzioni adatte a diminuire le inevitabili deformazioni dovute al fatto che la superficie terrestre non è perfettamente sviluppabile in piano.

           Le proiezioni convenzionali (meglio dette rappresentazioni), infine, sono basate sulle relazioni matematiche esistenti fra i punti del globo terrestre e quelli corrispondenti sulla Carta. In tal modo, a seconda degli scopi che ci si propone, è possibile costruire Carte che rispettino uno dei tre requisiti già citati, cioè l'equidistanza l'equivalenza o l'isogonia.

8.6       Proiezioni pure

È questa la categoria delle proiezioni vere e proprie, che possono essere sinteticamente suddivise in prospettiche e di sviluppo.

Nelle proiezioni prospettiche si immagina di proiettare il reticolo geografico su di un piano tangente o secante rispetto alla Terra, la quale per semplicità si suppone perfettamente sferica. Il punto da cui si immagina che fuoriescano le visuali si chiama punto di vista e si trova dalla parte diametralmente opposta al piano di proiezione (quadro), su cui si suppone di intercettare le suddette visuali. Sia il punto di vista che il quadro possono occupare infinite posizioni nello spazio, ma solo alcune di esse interessano in particolare.

Per il punto di vista si considerano quattro posizioni, che danno il nome ad altrettante proiezioni:

• centrografiche o gnomoniche, con punto di vista al centro della Terra;
• stereografiche, con punto di vista sulla superficie terrestre;
• scenografiche, con punto di vista a distanza finita dalla Terra;
• ortografiche, con punto di vista all'infinito.

In base alla posizione del quadro, invece, si parla di:

• proiezioni polari
• proiezioni equatoriali
• proiezioni oblique

a seconda che tale piano sia tangente ad un polo, ad un punto dell'Equatore o ad un punto qualsiasi della superficie terrestre.

Quindi, in definitiva, tenendo conto della posizione del punto di vista e del quadro, si potranno avere proiezioni centrografiche polari, equatoriali ed oblique, ovvero proiezioni stereografiche polari, equatoriali ed oblique ecc. (Figura 8.8).

Nelle proiezioni di sviluppo la superficie ausiliaria su cui si riporta il reticolo geografico è rappresentata da un cilindro o da un cono: perciò si parla di proiezioni cilindriche e proiezioni coniche (Figura 8.9).

Nelle proiezioni cilindriche il solido avvolgente la superficie terrestre si può immaginare tangente all'Equatore o secante lungo due paralleli intermedi; per cui l'asse terrestre viene ad essere coincidente con l'asse del cilindro. Sviluppando in piano la superficie laterale di tale solido, i meridiani si presentano come un fascio di rette tra loro parallele ed equidistanti, ortogonali all'Equatore; i paralleli, a loro volta, sono anch'essi rappresentati da un fascio di rette parallele tra loro e rispetto all'Equatore. In definitiva si ottiene un sistema di maglie rettangolari derivanti dall'intersezione di due sistemi di rette parallele, sistemi tra loro ortogonali. C'è da osservare che solo l'Equatore nella proiezione tangente o i due paralleli prescelti in quella secante presentano in Scala una lunghezza pari a quella reale, mentre gli altri paralleli, che sono riprodotti tutti con le stesse dimensioni, vengono ad essere proporzionalmente più lunghi di quelli reali; inoltre, i poli sono rappresentati da due linee e non da due punti.

Nelle proiezioni coniche, il solido ausiliario è rappresentato da un cono retto, la cui superficie laterale si immagina disposta sulla sfera terrestre e tangente a questa lungo un parallelo o secante lungo due paralleli. Sviluppando in piano questa superficie ausiliaria si ottiene un reticolato nel quale i paralleli sono rappresentati da archi di circonferenze concentriche ed il cui centro è anche il punto nel quale convergono i meridiani rettilinei, che sono dati dai raggi di queste circonferenze. Quindi le maglie del reticolato sono dei trapezi a basi curve, detti trapezoidi.

8.7       Proiezioni modificate e proiezioni convenzionali.

Come già è stato detto, le proiezioni pure possono essere soggette a modificazioni atte a ridurre le deformazioni introdotte nel passaggio dalla sfera terrestre al piano o alla superficie ausiliaria: si ottengono così le proiezioni modificate.

Tra le proiezioni convenzionali ricordiamo innanzitutto la rappresentazione conforme di Gauss (detta anche cilindrica trasversa di Mercatore) (Figura 8.14). Essa può essere considerata come pseudocilindrica: in questo caso però il cilindro avvolgente la superficie terrestre si deve supporre tangente non all'Equatore ma ad un meridiano, per cui l'asse del cilindro risulterà ortogonale all'asse terrestre; ne consegue che sarà possibile considerare infiniti cilindri tangenti alla superficie della Terra, perché infiniti sono i meridiani che si possono tracciare su di essa. Sviluppando in piano il cilindro considerato, il meridiano di tangenza e l'Equatore si presentano come due linee rette tra loro ortogonali, mentre gli altri meridiani ed i paralleli sono rappresentati da linee curve simmetriche rispettivamente al citato meridiano ed all'Equatore.

Le relazioni matematiche utilizzate nella costruzione rendono questa rappresentazione conforme; infatti, i meridiani ed i paralleli sono tracciati in modo da formare tra di loro degli angoli retti, come avviene nella realtà sulla superficie terrestre.

In questa rappresentazione le deformazioni lineari e superficiali aumentano notevolmente non appena ci si discosti dal meridiano di tangenza, lungo il quale è rispettata l'equidistanza. Si è visto che il massimo di Longitudine accettabile per evitare deformazioni non più tollerabili è di 6 gradi, cioè di 3 gradi a Ovest e ad Est del meridiano di tangenza, detto perciò anche meridiano centrale; all'area ellissoidale di 6 gradi di Longitudine si da il nome di fuso.

Nelle due rappresentazioni di Figura 8.14, si immagina il cilindro tangente al meridiano di Greenwich (sopra) ed al corrispondente antimeridiano (sotto).

Questi sono quindi i soli ad essere rettilinei e quelli lungo i quali è rispettata l'equidistanza. Gli altri meridiani ed i paralleli sono costruiti in modo da intersecarsi secondo angoli retti, al fine di rendere isogona la rappresentazione.

Fra le rappresentazioni pseudoconiche meritano particolare attenzione la policonica e la poliedrica.

La prima si ottiene immaginando di suddividere il globo terrestre in tante zone sferoidali e di avviluppare ognuna con un tronco di cono retto, tangente al parallelo medio di ciascuna di esse. Sviluppando in piano tali superfici ausiliarie, si ottengono delle fasce in cui i paralleli sono rappresentati da archi di circonferenze a raggio diverso; per cui queste fasce risultano contigue fra loro solo lungo il meridiano centrale, che è rettilineo, mentre le estremità sono sempre più distanziate man mano che si procede verso i lati. Questa proiezione è utilizzata per le Carte corografiche e per particolari Carte geografiche, fra cui la Carta Internazionale del Mondo al milionesimo.

La proiezione poliedrica, detta anche policentrica, si ottiene immaginando di avvolgere la Terra con un poliedro avente un elevato numero di facce, ognuna delle quali è tangente ad una piccola porzione della superficie terrestre: in tal modo ogni maglia (trapezoidale) del reticolato è indipendente da quelle vicine ed ha un piano di proiezione proprio. Le deformazioni vengono distribuite alla periferia di ogni maglia e pertanto sono piccole.

Infine, un posto a parte occupano le rappresentazioni interrotte o discontinue, che consistono spesso in proiezioni pseudocilindriche eseguite con accorgimenti particolari, in modo da ottenere in planisfero una buona rappresentazione dei continenti. Per ciascuno di questi si disegna un reticolato geografico indipendente: al posto di un meridiano centrale unico se ne sceglie uno per ogni continente ed in base ad esso si tracciano a sinistra e a destra gli altri meridiani, che formano così altrettanti fusi; la continuità del planisfero viene interrotta in corrispondenza degli oceani (il contrario se si vuole una buona rappresentazione degli oceani). In tal modo si ottiene l'equivalenza e contemporaneamente si riducono le deformazioni, perché si utilizza soltanto la parte del reticolato che meno altera le forme.

Nella Figura 8.15 sono riportati due esempi di rappresentazioni convenzionali molto usate per i planisferi. La prima è una proiezione pseudocilindrica equivalente, che però altera fortemente le figure; la seconda ha l'inconveniente di una rappresentazione discontinua, ma consente di mantenere l'equivalenza e di ridurre le deformazioni delle figure.

8.8       La scelta della proiezione

Dopo aver esaminato i caratteri principali delle proiezioni geografiche ed aver accennato ai tipi più usati, ci si può domandare quale delle numerosissime proiezioni sia la migliore. In senso assoluto non esiste una proiezione migliore, in quanto nessuna di esse ci consente di ottenere una raffigurazione completamente fedele del nostro pianeta; infatti sappiamo che per quanto perfetta possa essere una Carta, non sarà mai allo stesso Tempo equidistante, equivalente e conforme. Quindi sarà necessario scegliere il tipo di proiezione volta per volta, a seconda dello scopo che ci si prefigge.

In generale si può dire che per zone ad alte latitudini si adattano meglio le proiezioni prospettiche (stereografica, centrografica ecc.); per zone poste a latitudini intermedie sono da preferire le proiezioni coniche; per regioni comprese fra i tropici sono più indicate le proiezioni cilindriche. Se poi si vogliono costruire Carte per la Navigazione marittima o aerea, che vengono utilizzate per stabilire le Rotte da seguire, è chiaro che si preferiranno le proiezioni isogone, soprattutto la conica di Lambert e la cilindrica di Mercatore.

Per gli atlanti, che raccolgono planisferi, mappamondi, Carte generali e Carte speciali a varia Scala, il tipo di proiezione varia da caso a caso; in generale, però, le rappresentazioni convenzionali sono quelle più usate.

8.9       Il simbolismo cartografico

Una Carta geografica, oltre ad essere ridotta e approssimata, è anche simbolica, poiché tanto le particolarità del terreno quanto i singoli oggetti geografici vengono raffigurati tramite simboli speciali, detti segni convenzionali. D'altra parte è anche chiaro che tali simboli saranno tanto più numerosi quanto più grande è la Scala della Carta cui si riferiscono; difatti, sulle Carte relative a zone ristrette di terreno, che non hanno subito una notevole riduzione nella rappresentazione cartografica, è possibile riportare un maggior numero di particolari che non su quelle relative a vaste aree della superficie terrestre raffigurate in dimensioni fortemente ridotte. In genere gran parte dei segni convenzionali sono riprodotti in calce o a lato della Carta geografica, accompagnati dal loro significato.

Si possono distinguere due tipi di segni convenzionali: quelli relativi alla planimetria e quelli riguardanti l'altimetria. Tra i primi possiamo distinguere i simboli relativi all'idrografia (fiumi, laghi, ghiacciai, lagune ecc.), dei quali vengono dati alcuni esempi nella Figura 8.16.

I segni convenzionali che si riferiscono alle vie di comunicazione (strade, ponti, viadotti, ferrovie ecc.), sono illustrati nella Figura 8.17.

I simboli che raffigurano le opere stabili (case, chiese, punti trigonometrici ecc.), sono esemplificati nella Figura 8.18; vi sono riportati i simboli usati per la rappresentazione degli abitati, degli opifici, delle costruzioni speciali e di particolari diversi (punti trigonometrici, quote ecc.). Sono riportati anche i segni convenzionali che indicano i limiti amministrativi.

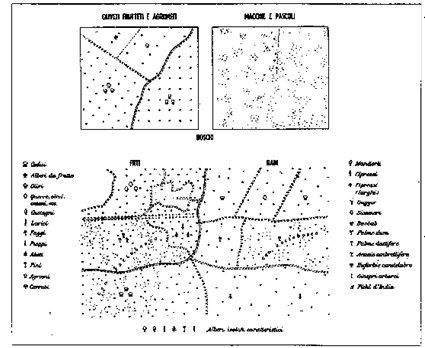
I simboli relativi alla vegetazione (boschi, macchie, campi ecc.), ai confini politici (stato) o amministrativi (regione, provincia, comune) ed alle proprietà (muri, recinti, limiti di colture ecc.), sono riprodotti nella Figura 8.19.

Il principio di costruzione delle Isoipse o curve di livello è il seguente: si immagina di intersecare il rilievo con tanti piani equidistanti, paralleli fra loro ed orizzontali; le linee di intersezione che si ottengono e che rappresentano appunto le curve di livello, vengono quindi proiettate sul piano della Carta (Figura 8.21).

In Figura 8.22 è riportato un esempio di Carta aeronautica per la navigazioneVFR.

Sulle Carte aeronautiche IFR il simbolismo è del tipo di quello riportato nella Figura 8.23.