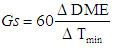Capitolo 7 - Unità di Misura e Distanze

7.1       Unità di misura. Cenni storici.

Nell'antichità il principale riferimento per la scelta delle unità di misura è sempre stato l'uomo: infatti sono stati utilizzati quali modelli e riferimenti, a seconda dei casi, parti del corpo umano, concetti ed oggetti derivanti dal suo ambiente di lavoro e di vita.

Soprattutto in epoche più antiche, la valutazione era spesso soggettiva: ci si riferiva, per esempio, a parti del proprio corpo. Pur non scomparendo mai totalmente questo tipo di valutazione, chiaramente diversa da un individuo ad un altro, a molte unità di misura si assegnarono presto valori ben precisi ed fissi per una determinata zona, costruendo campioni che fungevano da modelli, o dettando delle regole per la misurazione delle grandezze.

La determinazione delle regole da adottare e la costruzione, il possesso e la gestione dei campioni rappresentarono, in tutte le epoche, manifestazione del potere e, nel contempo, possibilità di esercitarlo e di aumentarlo: furono infatti prerogative, a seconda dei luoghi e delle epoche, di Imperatori, Re, Signori, Sacerdoti e talvolta anche di corporazioni di mercanti e artigiani. Se si esamina un elenco di unità di misura antiche di sufficiente ampiezza e completezza, si può rilevare quanto sia elevato il loro numero e diverso il valore attribuito a molte unità a seconda della località, dell'epoca e, persino, dell'impiego.

La determinazione del valore di ciascuna unità di misura in un determinato luogo è il risultato del contrasto fra la tendenza alla variazione e l'esigenza di stabilità presenti in ogni epoca. Si possono individuare molteplici cause di variazione del valore delle unità di misura; in particolare si ricordano: l'alterazione dei materiali con cui sono costruiti i modelli di riferimento, la distruzione o la scomparsa di questi sia per cause accidentali, sia per volontà dei detentori quando il fatto risulti per loro favorevole, variazioni di tecniche su cui è basata la determinazione dell'unità (per esempio delle modalità di aratura per alcune unità di superficie), cambiamenti delle abitudini di vita.

Ad esse si contrappone la necessità di mantenere stabili i valori (molto sentita soprattutto in alcuni strati della popolazione) per ragioni pratiche, per rispetto alla tradizione e, aspetto spesso assai rilevante, perché le variazioni si traducono molto spesso in aggravi dei tributi e dei servigi dovuti alle varie autorità.

Il contrasto fra queste due opposte tendenze ha dato, nel corso dei secoli, risultati assai diversi a seconda del tipo di unità di misura e dell'entità delle forze che si sono contrapposte. Per es. le unità di superficie non variavano per periodi relativamente lunghi soprattutto in zone dove la ridistribuzione periodica delle terre da parte del signore locale non era pratica comune, mentre maggiori variazioni subivano le unità di capacità, utilizzate negli scambi commerciali a tutti i livelli e per la determinazione dei tributi.

La varietà delle scelte operate e la diversità dei valori attribuiti alle unità di misura a seconda del luogo, dipendeva essenzialmente dal tipo di vita e dalle specifiche esigenze e situazioni sociali e commerciali di ciascuna popolazione. In ogni caso, però, la presenza in località diverse, anche della stessa area geografica, di unità diverse, (o aventi uguale denominazione ma diverso valore), per la valutazione di uno stesso prodotto o bene, rappresentava una fonte di difficoltà, complicazione e ingiustizia nei rapporti sociali ed economici.

In molte epoche si sono diffuse tendenze all'unificazione delle unità di misura su territori più o meno vasti. Tali tendenze si concretizzarono soprattutto in aree in cui era forte l'influenza di un centro commerciale o di manifestazioni commerciali di grande importanza, o in cui il commercio anche con mercati di altre aree geografiche era attività importante.

Iniziative in tal senso sono state portate avanti anche da numerosi Signori, Re ed Imperatori: gli interventi unificatori di autorità sui territori di loro competenza si susseguirono, con risultati assai diversi, in tutti i secoli (a cominciare, per esempio dagli interventi di Filippo il Macedone, Alessandro Magno e Giustiniano). Notevole rilevanza ebbero, in particolare, l'azione di Carlo Magno che emanò un decreto per uniformare i campioni delle unità di misura, gli interventi di principi e regnanti in epoca rinascimentale (soprattutto in Spagna, Francia, Russia, Polonia) e quelli realizzati nel sec. XVIII soprattutto nell'Europa centro-settentrionale. Ma il tentativo decisivo di unificazione su una vasta area risale solamente alla fine del Settecento: è del 1799, infatti, la definitiva adozione del sistema metrico decimale da parte della Repubblica Francese, anche se per la sua reale introduzione nel paese i tempi sono stati molto più lunghi. Il sistema metrico decimale si diffuse gradualmente negli stati europei durante tutto il secolo XIX, sostituendo le unità tradizionali; nel secolo successivo fu adottato, sia pure in modo incompleto e non omogeneo, da moltissime nazioni extraeuropee.

La più rilevante opposizione ufficiale al sistema metrico decimale si manifestò nei paesi anglosassoni e, in particolare, in Gran Bretagna, dove questo è stato accettato solo recentemente e dove sono ancora in uso le misure tradizionali.

Il Sistema Internazionale è quello che grazie alla scelta più opportuna delle unità fondamentali, si accosta il più possibile tanto alle esigenze scientifiche quanto a quelle pratiche. È stato approvato nel 1960 dalla Conferenza Generale dei Pesi e Misure, ed accettato da tutte le nazioni aderenti alla convenzione del metro. Questo sistema di unità è in corso di graduale introduzione anche in paesi tradizionalmente legati a sistemi di unità anglosassoni.

Il Sistema Internazionale si basa sul principio di individuare un numero minimo di grandezze fondamentali e di stabilire per queste le relative unità di misura; vengono inoltre stabilite le unità di misura di tutte le grandezze derivate; tutti i multipli e sottomultipli sono potenze del 10 della grandezza fondamentale; cosa che non si verifica per le grandezze del sistema anglosassone, e che costituisce il principale ostacolo al loro semplice uso.

In campo aeronautico, per la misurazione delle distanze viene generalmente usato il miglio nautico, per le altezze il piede, per le velocità il nodo; tutte unità del sistema anglosassone.

Alcuni paesi come la Cina e i paesi della ex Unione Sovietica per le quote adoperano i metri e non i piedi, per le velocità del vento i metri al secondo o i Km/Ora e non i nodi; la visibilità viene fornita negli U.S.A. in miglia statutarie non in metri come in Europa, le temperature vengono fornite in gradi Fahrenheit e non Celsius, ecc.

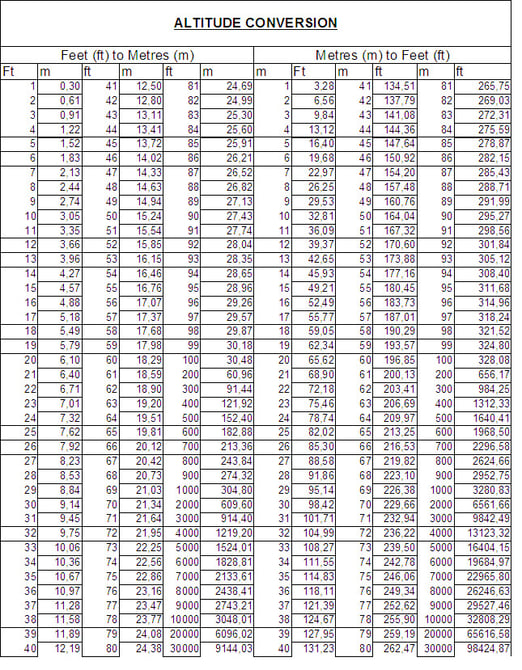
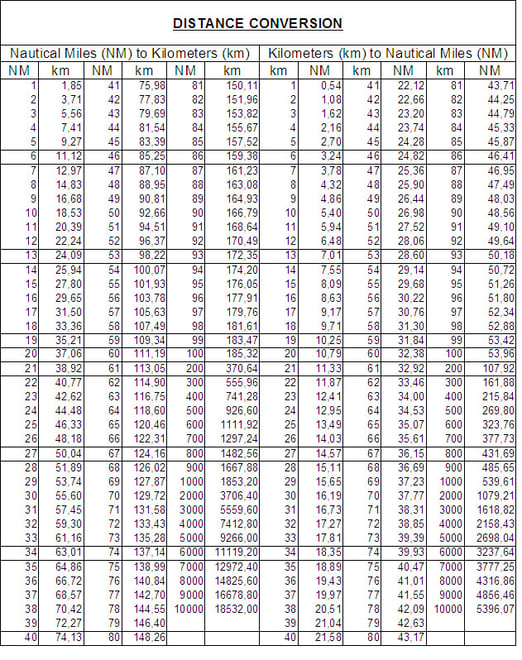
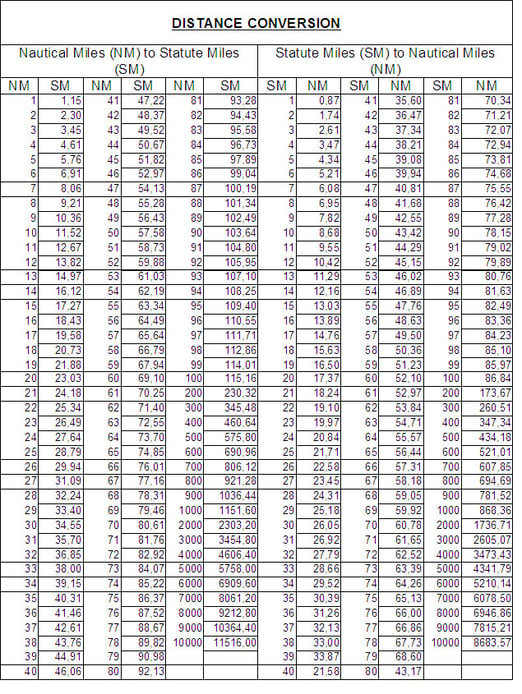
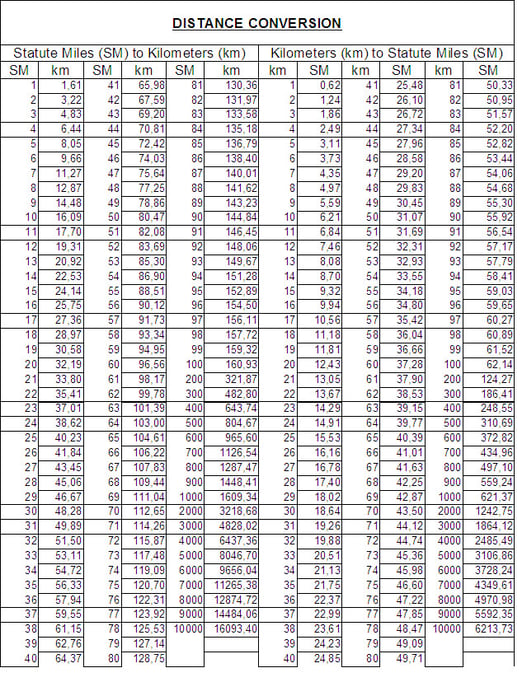
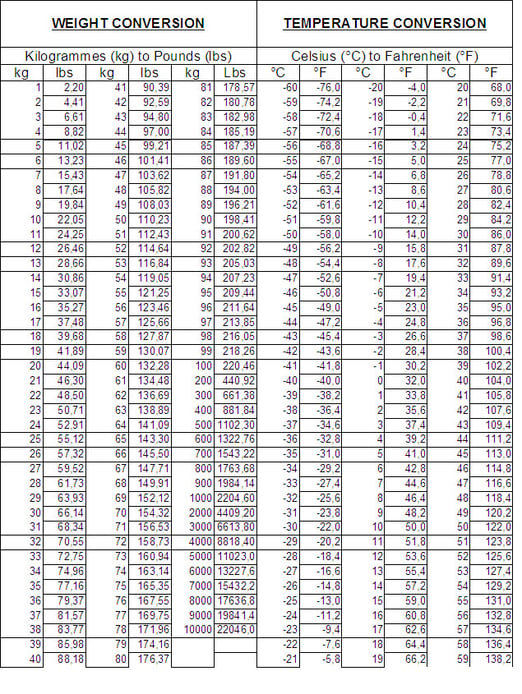
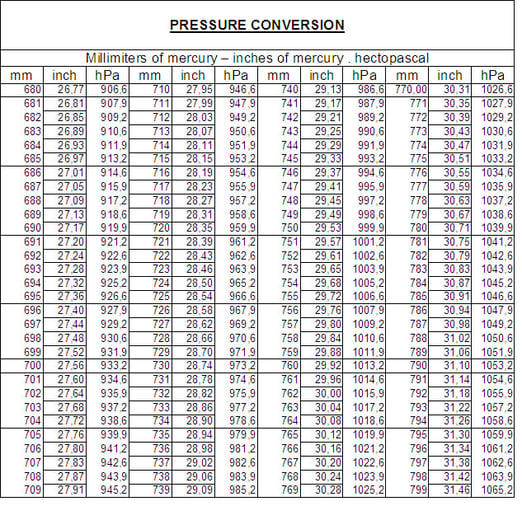
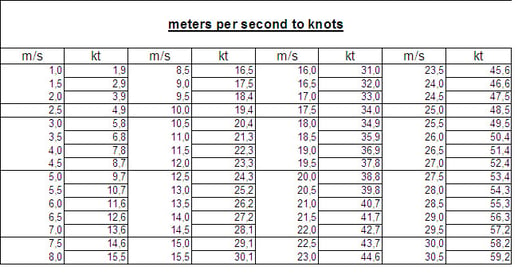
Fino a quando tutto il mondo non si sarà uniformato ad un unico standard, occorre munirsi di tabelle di conversione come quelle riportate nelle pagine seguenti per passare da un'unità di misura ad un'altra.

L'origine storica del nodo quale unità di misura della velocità risale all'epoca velica. Quando il comandante di un veliero voleva conoscere la propria velocità, faceva filare a poppa una sagola, sulla quale erano presenti dei nodi distanziati fra loro di 1/120 di miglio (15.433m). Alla estremità della sagola affondata, era fissata una tavoletta (solcometro a barchetta), che fungeva da ancora galleggiante (Figura 7.1).

In tal modo mentre il veliero avanzava, la sagola si svolgeva fuoribordo facendo sfilare un nodo dopo l'altro. Dopo 30 secondi di clessidra (30") venivano contati quanti nodi erano passati, che così rappresentavano con molta approssimazione la velocità della nave.

Di seguito due immagini di antichi campioni di unità di misura (Figura 7.2 e 7.3).

7.2       Determinazione della Velocità al suolo.

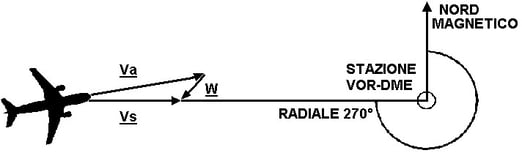
Un metodo per il calcolo della velocità dell'aereo rispetto al suolo è quello che si basa sull'uso del DME quando si vola in avvicinamento o in allontanamento rispetto ad una stazione VOR-DME o TACAN, mantenendosi su una radiale costante (Figura 7.4)

Occorre effettuare due letture del DME a distanza di tempo determinata con precisione, e poi rapportare la Distanza ottenuta all'ora, per avere l'effettiva velocità al suolo.

Esempio.

Volando verso una stazione VOR-DME mantenendo una Radiale costante si ha che alle ore 13:12 il DME indica 133.5 e dopo 1 minuto alle 13:13 indica 125.5.

Determinare la GS.

Se in un minuto si sono percorse 8 miglia nautiche, in 60 minuti si percorreranno:

8 * 60 = 480 miglia

La velocità al suolo è di 480 nodi.

Occorre ricordare che il DME misura la Distanza effettiva tra l'aereo e la stazione (Slant range), mentre per il calcolo della ground speed avremmo bisogno della variazione di Distanza della proiezione al suolo della posizione dell'aereo nell'unità di Tempo (Figura 7.5).

L'errore commesso può essere considerato trascurabile quando la Distanza dell'aereo dalla stazione espressa in miglia è superiore alla quota in migliaia di piedi, ovvero 10 miglia per un aereo a 10.000 piedi o 35 miglia per un aereo a FL 350.

La velocità esprime il valore della variazione di una Distanza con il Tempo.

ovvero usando il simbolismo matematico:

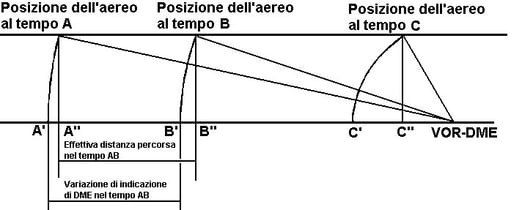
Con riferimento alla Figura 7.5, per il calcolo esatto della velocità occorrerebbe conoscere il valore di Distanza percorso nell'intervallo di Tempo AB. Questo valore è pari alla Distanza A"B". La lettura di due valori di DME fornisce invece la Distanza A'B'.

I valori di distanza A'B' e A"B" sono molto vicini, e tendono a divenire uguali con l'aumento della Distanza dalla stazione. A distanze ravvicinate, invece l'errore diventa notevole.

Si può vedere dalla figura che la Distanza B"C" è notevolmente diversa da quella B'C' ricavata dalla lettura del DME al Tempo B e al Tempo C in prossimità della stazione.

In quest'ultimo caso i calcoli della velocità al suolo sarebbero grossolanamente errati.

Esempio.

Determinazione dell'errore percentuale commesso nel calcolo della Velocità al suolo per un aereo che vola su Radiale costante verso una stazione VOR-DME ad una quota costante di 10.000 piedi:

     caso 1: letture effettuate a 35 e 30 DME

     caso 2: letture effettuate a 15 e 10 DME

     caso 3: letture effettuate a 7 e 2 DME

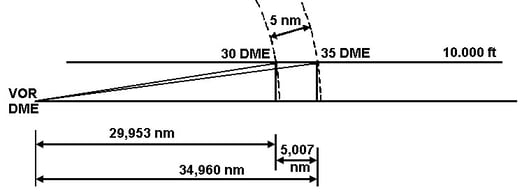
Caso 1: l'angolo a formato tra il piano orizzontale e la congiungente aereo-stazione DME è determinabile per mezzo di semplici calcoli trigonometrici (Figura 7.6).

sen a = quota aereo / lettura DME

Sia la quota che la distanza dalla stazione devono essere espressi con la stessa unità di misura.

10.000 piedi = 1,66 miglia nautiche

a35DME = arc sen (1,66 / 35) = 2°43'

a30DME = arc sen (1,66 / 30) = 3°11'

Le due effettive distanze dalla stazione saranno esprimibili come prodotto della Distanza DME per il coseno dell'angolo relativo.

d35DME = 35 cos 2°43' = 34,960

d30DME = 30 cos 3°11' = 29.953

Si vede che a fronte di due letture che differiscono di 5 miglia l'effettivo percorso dell'aereo è Stato di 5,007 miglia.

L'errore commesso è:

e = 5,000 - 5,007 = -0.007 miglia

L'errore percentuale è:

e% = (-0,007 / 5,007) * 100 -0,14%

L'errore che discende dalla lettura della Slant distance al posto della effettiva distanza, in questo primo caso è la causa di un errore sulla distanza talmente piccolo che è sicuramente inferiore agli errori causati dalle imprecisioni proprie del DME e di errori di lettura del cronometro tra le due posizioni.

L'errore sulla distanza si ripercuote integralmente sull'errore nella velocità. Un errore dello -0,15% equivale ad un errore nel calcolo della velocità di meno di un nodo per un aereo che vola con una ground speed di 500 nodi.

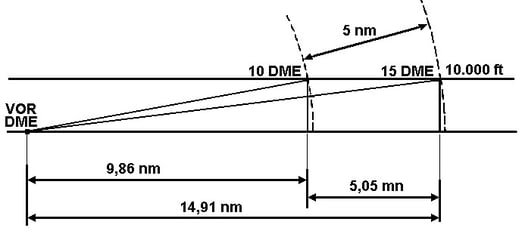
Caso 2: abbiamo due letture DME a 15 e 10 miglia dalla stazione (Figura 7.7). Gli angoli formati tra il piano orizzontale e la congiungente aereo-stazione DME saranno:

a15DME = arc sen (1,66 / 15) = 6°23'

a10DME = arc sen (1,66 / 10) = 9°36'

Le due effettive distanze dalla verticale della stazione saranno:

d15DME = 15 cos 6°23' = 14,91

d10DME = 10 cos 9°36' = 9.86

L'effettivo percorso dell'aereo è stato:

14,91 - 9,86 = 5,05 miglia

a fronte delle 5 miglia indicate dal DME

L'errore commesso è:

e = 5,00 - 5,05 = -0.05 miglia

L'errore percentuale è:

e% = (-0,05 / 5,05) * 100 -1%

Anche in questo caso l'errore è molto piccolo e praticamente trascurabile essendo dell'ordine dei 5 nodi per una Gs di 500 nodi.

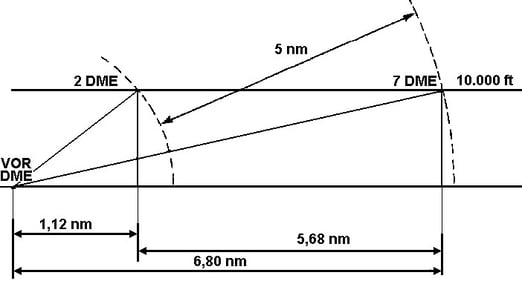
Caso 3: nell'ultimo caso abbiamo due letture DME a 7 e 2 miglia dalla stazione (Figura 7.8). Gli angoli formati tra il piano orizzontale e la congiungente aereo-stazione DME saranno:

a7DME = arc sen (1,66 / 7) = 13°43'

a2DME = arc sen (1,66 / 2) = 56°06'

Le due effettive distanze dalla verticale della stazione saranno:

d7DME = 7 cos 13°43' = 6,80

d2DME = 2 cos 56°06' = 1,12

L'effettivo percorso dell'aereo è stato:

6,80 - 1,12 = 5,68 miglia

a fronte delle 5 miglia indicate dal DME

L'errore commesso è:

e = 5,00 - 5,68 = -0.68 miglia

L'errore percentuale è:

e% = (-0,68 / 5,68) * 100 -12%

L'errore in questo caso è notevole, ed in grado di viziare notevolmente il calcolo della velocità.

7.3       Determinazione della Distanza dal traverso di una stazione.

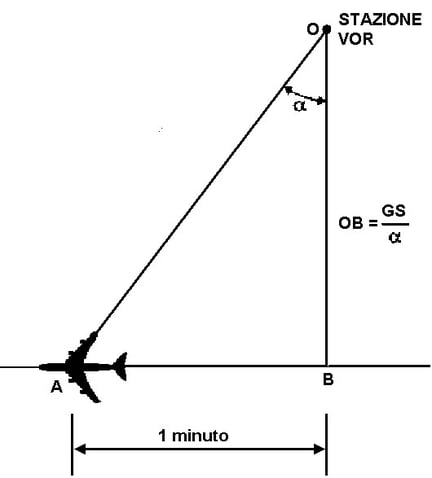
Esiste un sistema molto semplice per calcolare la Distanza da una stazione: nel momento in cui questa si trova al traverso, mantenendo volo rettilineo si fa partire il cronometro. Dopo un minuto si vede di quanti gradi dietro al traverso si trova la stazione (Figura 7.9).

La Distanza in miglia è data dalla formula:

Distanza OB = Gs / a

Distanza OB                =          Distanza al traverso della stazione

Gs                              =          velocità al suolo

a                                =          numero di gradi in un minuto

Per la dimostrazione della semplice formula sopra ricordata occorre effettuare alcuni passaggi matematici e ricordare alcune relazioni trigonometriche.

Dalla trigonometria abbiamo che:

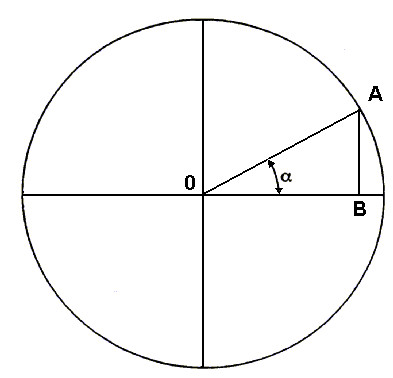
Consideriamo il segmento OA (Figura 7.10), ossia il raggio del cerchio, pari all'unità (OA=1). Abbiamo che il segmento AB è uguale al seno dell'angolo a e che il segmento OB è uguale al coseno dell'angolo a.

AB = sen a

OB = cos a

Nel caso in cui il segmento OA non sia unitario avremo:

AB = OA sen a

OB = OA cos a

Nel caso particolare in cui OA = 60 e a = 1° abbiamo che:

AB = 60 sen 1° = 60 0.0175 = 1,05 (valore molto vicino all'unità)

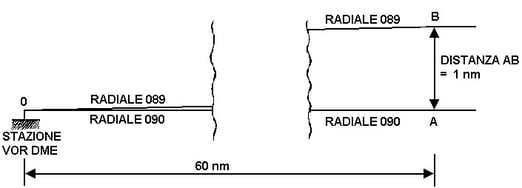
Questa relazione matematica trasferita nel mondo pratico ci fornisce una semplice relazione tra piccoli angoli e distanze. Per esempio a 60 miglia da una stazione VOR la Distanza tra due radiali contigui è di circa un miglio, a 120 miglia è di circa 2 miglia (Figura 7.11). Il valore è approssimato, ma l'errore commesso è trascurabile, in quanto dell'ordine del 5%.

Per angoli maggiori, fino a 10 gradi, la relazione continua a mantenere la sua validità. Per esempio, nel caso di un angolo di 10 gradi abbiamo:

AB = 60 sen 10° = 60 0,1736 = 10,4 10 miglia nautiche

La relazione sopra riportata discende dalla constatazione che per piccoli angoli:

sen a  a 

a espresso in radianti

1 radiante = 57°17'45"         (valore prossimo a 60 gradi)

Se esprimiamo l'angolo in gradi abbiamo che:

sen (57°17'45" a) sen (60 a) 60 sen a a

da cui:

Abbiamo a questo punto la possibilità di esprimere la Distanza AB in due modi: o come il prodotto della velocità al suolo Gs moltiplicato per il Tempo T, o come prodotto della Distanza OB per il seno dell'angolo a, che come abbiamo visto può essere espresso come a / 60.

AB = Gs T = OB sen a = OB (a / 60)

Gs       =          velocità in nodi         =          miglia nautiche / ora

T          =          Tempo in minuti

OB       =          Distanza dalla stazione in miglia nautiche

sen a  =          valore numerico puro

a          =          valore numerico in gradi

Essendo Gs misurata in miglia nautiche / Ora, ed il Tempo in minuti, occorre trasformare la velocità in miglia al minuto in modo da rendere le unità di misura omogenee.

La velocità in miglia al minuto sarà uguale a Gs / 60.

A questo punto abbiamo che:

(Gs / 60) T = OB (a / 60)

da cui:

Gs T = OB a

OB = Gs T / a

Nella pratica, se si assume T = 1 minuto, avremo che volando al traverso della stazione sarà sufficiente contare quanti radiali si sono attraversati in un minuto per ottenere la Distanza OB dalla stazione utilizzando la semplice relazione:

OB = Gs / a

Gs espresso in nodi, a in gradi e OB in miglia nautiche.