Capitolo 4 - Il Tempo e la sua Misura

4.1       Giorno sidereo, Giorno solare vero, Giorno solare medio.

Il Tempo è una grandezza fisica il cui scorrere viene avvertito istintivamente dai sensi degli esseri umani. E' d'altra parte una grandezza non misurabile direttamente, ma soltanto per il tramite della misurazione dello spazio percorso da un corpo in movimento uniforme o mediante il conteggio di un succedersi regolare di eventi, siano essi le oscillazioni di un pendolo o quelle di un cristallo di quarzo fatto vibrare da un campo magnetico alternato.

Fin dall'antichità è apparso chiaro che uno dei moti fondamentali a cui si può fare riferimento è quello che la sfera celeste e il Sole compiono intorno all'asse della Terra nel corso di una giornata. Su questo moto sono stati e sono tuttora regolati gli orologi, che costituiscono i mezzi meccanici od elettronici con cui in pratica si effettua il computo del Tempo.

Poiché il movimento degli astri non è che un'apparenza dovuta alla rotazione della Terra, in definitiva possiamo assumere questo moto rotatorio come base per le nostre misure: esso rappresenta l'orologio più naturale che abbiamo a disposizione, e ci consente di fissare una delle principali unità di misura del Tempo: il Giorno.

Comunemente per Giorno si intende il periodo di Tempo che la Terra impiega per compiere una rotazione intorno al suo asse: però a seconda che tale rotazione venga computata facendo riferimento alle stelle oppure al Sole, si deve fare una distinzione tra Giorno sidereo e Giorno solare, che sono di durata leggermente diversa.

Il Giorno sidereo rappresenta la durata effettiva della rotazione terrestre rispetto alle stelle fisse, ed ha la durata di 23 ore, 56 minuti e 4 secondi-

Il Giorno solare, riferito al Sole medio, invece che alle stelle, ha una durata di 24 ore.

Questa differenza di 4 minuti circa dipende dal fatto che mentre la Terra compie una rotazione, si muove anche di un certo tratto lungo la sua orbita; perciò per rivedere il Sole nella stessa direzione, dopo che la Terra ha fatto un giro completo intorno al proprio asse, occorre che essa compia un supplemento di rotazione corrispondente all'arco percorso sull'orbita.

Il Giorno sidereo rappresenta il vero periodo della rotazione terrestre e può considerarsi di durata praticamente costante, essendo le variazioni dovute ad irregolarità di questo movimento estremamente piccole.

La durata del Giorno solare vero invece non è sempre la stessa nel corso dell'Anno, poiché la Terra descrive la sua orbita intorno al Sole con velocità variabile: in prossimità del perielio la velocità è massima, ed il Giorno solare vero supera di alcuni secondi le 24 ore; in prossimità dell'afelio la velocità orbitale diminuisce ed il Giorno solare vero dura un po' meno di 24 ore.

Nonostante questa variabilità, noi usiamo comunemente il Giorno solare, perché i ritmi della nostra vita sono regolati dal movimento del Sole, e dall'alternarsi del Giorno e della notte.

Per ovviare all'inconveniente della durata variabile del Giorno nei vari periodi dell'Anno, ci serviamo del Giorno solare medio, che risulta dalla media delle durate di tutti i giorni dell'Anno e corrisponde a 24 ore esatte. Su di esso sono regolati i nostri orologi, ed il secondo, che è la 1/86.400 parte del Giorno medio viene assunto come unità di misura (Figura 4.2).

L'angolo misurato in Tempo tra il Sole medio e il Sole vero è ricavabile da apposite tabelle o grafici, che riportano i valori della cosiddetta equazione del Tempo (Figura 4.3).

4.2       Ora Vera Locale, Ora Media Locale.

Per effetto della rotazione terrestre, nel periodo di un Giorno il Sole vero passa davanti a tutti i Meridiani geografici impiegando circa un'Ora per spostarsi di 15 gradi di Longitudine, 4 minuti per ogni grado e 4 secondi per ogni primo. Questi valori sono esatti e costanti per il Sole medio.

Ogni Meridiano ha il suo Tempo vero, che è diverso da quello di tutti gli altri: tutti i punti situati sullo stesso Meridiano hanno il mezzogiorno solare nel medesimo istante, cioè nel momento della culminazione del Sole vero, o passaggio del Sole vero al Meridiano. Nei luoghi posti ad Est il mezzogiorno è già passato, in quelli posti a Ovest deve ancora venire.

Si definisce Ora vera locale l'angolo orario misurato a partire dall'antimeridiano dell'osservatore fino alla direzione del Sole vero, in senso orario.

Nella Figura 4.6 si immagina di osservare la sfera terrestre dalla verticale del polo Nord. L'antimeridiano del punto A è evidenziato con linea tratteggiata.

Similmente si definisce Ora media locale l'angolo orario compreso tra l'antimeridiano dell'osservatore e il Sole medio (Figura 4.7).

In entrambi i casi l'angolo viene misurato a partire dall'antimeridiano dell'osservatore in senso orario; nel caso dell'Ora vera locale, l'angolo è quello riferito al Sole vero, nel caso dell'Ora media locale l'angolo è riferito al Sole medio.

La differenza di Ora locale (media o vera) tra due osservatori posti su due Meridiani differenti è pari alla loro differenza di Longitudine (Figura 4.8).

Dl = DT

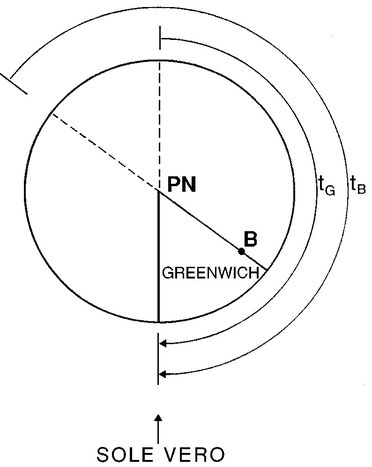
4.3       Tempo medio di Greenwich.

L'Ora media locale degli osservatori che si trovano sul Meridiano di Greenwich viene chiamata Greenwich Mean Time o Ora media di Greenwich, ed è presa quale riferimento per la misurazione del Tempo (Figura 4.9).

Conoscendo il Greenwich Mean Time è facile determinare l'Ora media locale per ogni altro osservatore sulla Terra; infatti sapendo che Dt = Dl, e dato che la Longitudine di Greenwich è 0, abbiamo che:

Dt = l

Occorre perciò trasformare la Longitudine da arco a Tempo, e sommarla algebricamente al GMT, ricordando che i punti situati ad Est di Greenwich hanno l'Ora media locale maggiore:

Tempo medio locale LMT = GMT + l

Per i punti situati a Ovest di Greenwich avremo invece:

Tempo medio locale LMT = GMT - l

Si può anche dire che al fine di ottenere il Tempo medio locale è sufficiente sommare la Longitudine trasformata in Tempo al GMT, con l'avvertenza di ricordare che le longitudini Est hanno segno positivo, quelle Ovest segno negativo.

LMT = GMT + l

lE       =          +

lW      =          -

4.4       Tempo Fuso, Fusi Orari.

L'Ora media locale, benché uniforme, e pur rappresentando un progresso rispetto all'Ora vera locale, non è adatta per regolare i rapporti tra località situate a longitudini diverse, ed è perciò estremamente scomoda anche nell'ambito di un singolo Stato.

In passato alcuni stati decisero di adottare per tutto il loro territorio un'Ora convenzionale unica, detta Ora nazionale, corrispondente generalmente a quella vera del Meridiano passante per la relativa capitale.

Anche facendo ricorso all'Ora nazionale, non era possibile risolvere le complicazioni derivanti dal fatto che nel passare da uno Stato ad un altro si potevano avere non solo differenze di ore, ma anche di minuti e secondi.

Si è resa quindi necessaria l'adozione di un sistema ideato nel 1859 dall'astronomo italiano Quirio Filopanti e codificato da una convenzione internazionale nel 1893.

La superficie terrestre è stata divisa in 24 spicchi, detti Fusi Orari, limitati da Meridiani distanti 15° in Longitudine e quindi con differenze di un'ora l'uno dall'altro.

Per tutti i luoghi situati entro un determinato Fuso è stato assunto convenzionalmente, come Tempo civile, quello che corrisponde al Meridiano centrale del Fuso.

Il Fuso Zero si estende per 7 gradi e 30 primi ad Est e a Ovest del Meridiano di Greenwich, che viene considerato come riferimento ed è detto Tempo medio di Greenwich, GMT o anche Zulu Time.

In tutti i punti situati all’interno del fuso, gli orologi saranno regolati in modo da segnare contemporaneamente mezzogiorno quando il Sole medio culmina sul Meridiano fondamentale (Figura 4.13).

Tutti i paesi come l'Italia, situati nel Fuso immediatamente ad Est del Fuso Zero, adottano l'Ora del relativo Meridiano centrale e hanno quindi un Tempo civile pari a GMT + 1.

Muovendosi ulteriormente verso Est, i paesi del Fuso avente il 30° Est quale riferimento, adottano un'Ora pari a GMT + 2, e così via.

Come si può osservare dalla Figura 4.14, (tratta da http//aa//usno.navy.mil/AA) i limiti effettivi dei Fusi Orari non sono segnati dai Meridiani, ma se ne discostano per seguire i confini politici, in modo da permettere ad alcuni stati di avere la stessa Ora adottata su tutto il paese.

Inoltre, alcuni paesi hanno adottato un Tempo particolare, dato dal GMT aumentato o diminuito di una quantità non corrispondente ad un numero intero di ore, come per esempio l'India che ha adottato un Tempo pari a GMT + 5:30, l'Iran GMT + 3:30, ecc.

4.5       Ora Legale, Ora Estiva.

L'Ora Legale è l'ora adottata per legge all'interno di uno Stato.

Questa coincide generalmente con l'Ora Fuso.

Nel linguaggio comune per Ora Legale si intende invece l'Ora Estiva, il periodo cioè in cui l'ora legalmente in uso viene modificata di sessanta minuti.

Per motivi di risparmio energetico, molti stati adottano durante i mesi estivi la cosiddetta "Ora Legale" o meglio Ora Estiva (Daylight Saving Time) al fine di poter usufruire più a lungo della luce solare ed avere così un minore consumo di energia elettrica.

L'operazione viene compiuta generalmente in primavera spostando le lancette degli orologi in avanti di un'ora in modo da far loro segnare l'ora del Fuso immediatamente più ad Est.

Per esempio nell'Europa centrale si passa da GMT + 1 a GMT + 2; a New York si passa da GMT - 5 a GMT - 4. Alla fine dell'estate si riportano le lancette indietro di un’ora.

Esempi.

Calcolare la differenza di orario tra Roma e New Orleans

Roma = GMT + 1

New Orleans = GMT - 6

La differenza è di 7 ore.

Calcolare la differenza di orario tra Roma e Rio de Janeiro durante l'estate nell'emisfero Nord.

Roma = GMT + 2 (Ora estiva)

Rio de Janeiro = GMT - 3

La differenza è di 5 ore.

Calcolare la differenza di orario tra Roma e Rio de Janeiro durante l'inverno nell'emisfero Nord.

Roma = GMT + 1

Rio de Janeiro = GMT - 2 (Ora estiva)

La differenza è di 3 ore.

4.6       Tempo Universale Coordinato (UTC)

Con l'avvento degli orologi atomici, si è avuta la possibilità di misurare il Tempo in modo estremamente preciso, ed in maniera non più legata al moto della Terra.

Il secondo atomico viene infatti definito come Tempo corrispondente a 9.192.631.770 cicli di una particolare radiazione emessa dal cesio.

L'UTC è una evoluzione del GMT, derivata dallo sganciamento della misurazione del Tempo dal moto della Terra, così come per il metro non ci si avvale più della sbarra campione di platino-iridio conservata a Parigi.

L'UTC è corrispondente al GMT per tutti gli scopi pratici; esso è ricavato dal confronto di tempi atomici di numerosi laboratori in varie parti del mondo; è misurato e mantenuto da due specifici laboratori: il British Royal Observatory e l'U.S. Naval Observatory.

A seguito dell'adozione dell'UTC, e a causa della sua estrema precisione e costanza, periodicamente è necessario introdurre un secondo detto bisestile per rifasare questo Tempo con l'esatta posizione della Terra, la quale ha una velocità di rotazione che non può più essere considerata esattamente costante.

La velocità di rotazione della Terra infatti a causa delle perturbazioni gravitazionali subisce delle leggere variazioni, dell'ordine del millisecondo al giorno; inoltre la velocità di rotazione decresce lentamente per effetto dell'energia dissipata con i moti legati ai fenomeni di marea provocati dalle forze gravitazionali del Sole e della Luna. In un giorno molto lontano anche la Terra si fermerà, così come ha già fatto la Luna da epoche remote.

4.7       Linea cambiamento data.

L'antimeridiano di Greenwich divide il suo Fuso in due parti, aventi la stessa Ora ma data diversa (Figura 4.15).

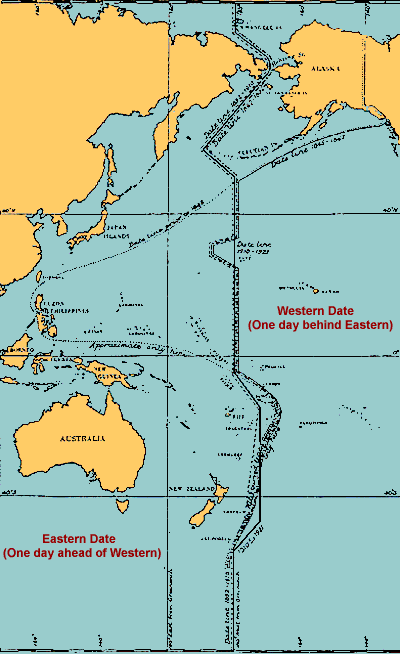
La linea cambiamento data coincide solo in parte con questo in quanto il suo andamento è stato modificato in modo da farla passare sempre su zone marine o disabitate (Fig.4.16).

Quando il Sole medio passa per il Meridiano di Greenwich, alle 12:00 UTC, tutto il mondo ha la stessa data (Figura 4.17).

Con il passare delle ore la situazione si modifica così come rappresentato in Figura 4.18 alle ore 18:00 UTC

Alle ore 00:00 UTC la situazione è quella di Figura 4.19.

Dopo altre sei ore alle 06:00 UTC la situazione è quella di Figura 4.20.

Esempio 1.

A Hong Kong sono le ore 18:00 (zone time = UTC + 8).

Determinare l'Ora di Tunisi e di New York.

UTC = 18:00 - 08:00 = 10:00

Ora di Tunisi = UTC + 1 = 10:00 + 01:00 = 11:00

Ora di New York = UTC - 5 = 10:00 - 05:00 = 05:00

Esempio 2:

A Roma sono le 22:00 del Giorno 10.

Determinare la data e l'Ora a San Francisco e a Delhi.

Ora di Roma = UTC + 1

UTC = 22:00 - 01:00 = 21:00

Ora di San Francisco = UTC - 9 = 21:00 - 09:00 = 12:00 del Giorno 10

Ora di Delhi = UTC + 05:30 = 21:00 + 05:30 = 26:30

26:30 - 24:00 = 02:30 del Giorno 11

Esempio 3:

A Perth sono le ore 22:00 del Giorno 20 (Ora estiva).

Determinare la data e l'Ora di Città del Messico.

Perth si trova nel Fuso UTC + 8

Con l'Ora legale adotta l'Ora del Fuso UTC + 9

UTC = 22:00 - 09:00 = 13:00

Ora di Città del Messico = UTC - 6 = 13:00 - 06:00 = 07:00 del Giorno 20

Esempio 4:

A Tokyo sono le ore 06:00 del Giorno 15.

Determinare la data e l'Ora di Chicago.

Ora di Tokyo = UTC + 9

UTC = 06:00 - 09:00 (+ 24:00) = 21:00 del Giorno 14

Ora di Chicago = UTC - 6 = 21:00 - 06:00 = 15:00 del Giorno 14

Esempio 5:

A Fairbanks in Alaska sono le ore 12:00 del Giorno 31.

Determinare la data e l'Ora alle isole Maldive.

Ora di Fairbanks = UTC - 10

UTC = 12:00 + 10:00 = 22:00 del Giorno 31

Ora delle Maldive = UTC + 5:30 = 22:00 + 05:30 = 27:30

27:30 - 24:00 = 03:30 del Giorno 1 del mese successivo

4.8       Alba, Sorgere e Tramonto del Sole, Crepuscoli.

L'alba è la luminescenza che precede il sorgere del Sole.

Si parla di sorgere del Sole, riferendosi al momento in cui il Sole al mattino compare da sotto l'orizzonte.

Il tramonto corrisponde invece al momento della scomparsa del Sole sotto l'orizzonte.

Ogni osservatore ha un diverso orizzonte, funzione principalmente della sua elevazione sulla superficie terrestre (Figura 4.21).

La Figura precedente si riferisce all'orizzonte geometrico dell'osservatore.

A causa della rifrazione dei raggi luminosi, determinata dalla differente densità dell'atmosfera alle varie quote, (costantemente decrescente partendo da Terra e muovendosi verso l'alto), i raggi luminosi vengono incurvati leggermente verso il basso; per questo motivo l'orizzonte apparente o ottico è leggermente più alto del corrispondente orizzonte geometrico, ed è possibile osservare punti che si trovano ad una distanza superiore rispetto a quella dell'orizzonte geometrico (Figura 4.22).

L'orizzonte astronomico è un piano perpendicolare alla verticale dell'osservatore e passante per il centro della Terra (Figura 4.23).

Prima del sorgere del Sole si ha una transizione graduale dal buio completo della notte alla piena luce del mattino.

La stessa sequenza in ordine inverso sia ha alla sera dopo il tramonto, con la luminosità via via decrescente fino al buio totale.

Questo periodo di Tempo viene chiamato Crepuscolo; convenzionalmente viene considerato diviso in tre fasi (Fig.4.24):

           Crepuscolo civile: corrisponde al periodo di Tempo in cui il Sole si trova tra l'orizzonte (sorgere o tramonto) e 6 gradi sotto l'orizzonte.

Durante il Crepuscolo civile vengono accese le luci nelle strade, i fari delle automobili ecc. C'è ancora molta luce e le stelle non sono visibili.

           Crepuscolo nautico: corrisponde al periodo di Tempo in cui il Sole si trova tra 6 e 12 gradi sotto l'orizzonte.

Durante il Crepuscolo nautico è già abbastanza buio da poter osservare le stelle più luminose, ma c'è ancora abbastanza luce da poter distinguere l'orizzonte. Questo è importante per chi deve determinare la posizione di una imbarcazione mediante la misurazione con il sestante dell'altezza degli astri sull'orizzonte, con la conseguente necessità di avere visibili entrambi.

           Crepuscolo astronomico: corrisponde al periodo di Tempo in cui il Sole si trova tra 12 e 18 gradi sotto l'orizzonte.

Durante il Crepuscolo astronomico la luce è talmente poca da permettere l'osservazione astronomica delle stelle.

Quando si vuole calcolare l'Orario del sorgere o del tramonto del Sole, o del Crepuscolo, occorre ricordare che i valori forniti dalle tabelle sono di Tempo Medio Locale o LMT.

Il Local Mean Time è uguale al GMT per gli osservatori situati sul Meridiano di Greenwich, e al Tempo Fuso per gli osservatori situati sul Meridiano centrale del Fuso di appartenenza. Per tutti gli altri osservatori occorre effettuare una correzione di orario corrispondente alla differenza di Longitudine tra il Fuso di riferimento e l'osservatore.

Nella Figura 4.25 viene evidenziato che il LMT del sorgere del Sole è uguale per tutti gli osservatori.

Sapendo che il Sole sorge e tramonta prima, per gli osservatori situati a oriente del Meridiano di riferimento, e successivamente per gli osservatori ad occidente, avendo a disposizione il Tempo Medio Locale, e volendo calcolare il Tempo Fuso (che corrisponderà all'UTC per il Fuso Z), occorrerà sottrarre un valore in Tempo pari alla differenza di Longitudine per osservatori a Est del Meridiano di riferimento, e aggiungere un corrispondente valore di Tempo nel caso contrario (Fig.4.26).

Tempo Fuso = LMT - t

t = segno positivo per osservatore ad Est del meridiano di riferimento

t = segno negativo per osservatore ad Ovest del meridiano di riferimento

Al fine del calcolo dell'Ora del sorgere e del tramonto del Sole è possibile usare una tabella semplificata che fornisce dati ad intervalli abbastanza ampi ma validi per tutto l'anno come quella di seguito riportata.

NOTA: i tempi riportati sono riferiti al primo di ogni mese ed espressi in Tempo Medio Locale. Per la loro conversione in UTC aggiungere (longitudini Ovest) o sottrarre (longitudini Est) l’intervallo di tempo corrispondente all’arco di longitudine del luogo interessato

n.v. = non visibile s.v. = sempre visibile

Vengono riportati gli Orari in Tempo medio locale per il primo giorno del mese, e per valori di latitudini spaziati di 10 gradi; occorre interpolare per determinare l'Ora del sorgere e del tramonto per giorni e latitudini intermedie.

Per un calcolo più accurato vi sono tavole, del sorgere, del tramonto e dei Crepuscoli che riportano gli Orari ad intervalli inferiori.

Esempio 1.

Giorno 2 ottobre.

f = 70°00' N

= 012°15' E

Calcolare l'Ora Fuso del sorgere del Sole.

LMT del sorgere del Sole ricavato dalle tabelle = 06:17

Differenza di Longitudine tra il Meridiano centrale del Fuso ed il punto considerato:

15°00' - 12°15' = 02°45' (osservatore ad Ovest del Meridiano di riferimento).

02°45' arco = 11' Tempo

Tempo Fuso del sorgere del Sole = 06:17 + 00:11 = 06:28

Esempio 2:

Giorno 30 agosto (Ora estiva).

f = 35°00' N

= 018°00' E

Calcolare l'Ora Fuso del tramonto del Sole.

LMT del tramonto ricavato dalle tabelle mediante interpolazione: 18:30

Differenza di Longitudine tra il Meridiano centrale del Fuso e il punto considerato:

18°00' - 15°00' = 03°00' (osservatore ad Est del Meridiano di riferimento)

03°00' arco = 12' Tempo

Tempo Fuso del tramonto del Sole = 18:30 - 00:12 + 01:00 = 19:18

Esempio 3:

Giorno 11 ottobre.

f = 56°00' N

= 095°15' E

Calcolare l'Ora UTC del Crepuscolo civile mattutino.

LMT del Crepuscolo ricavato dalle tabelle: 05:45

Conversione della Longitudine in Tempo: 095°15' = 06:21

Tempo UTC del Crepuscolo civile mattutino = 05:45 + 06:21 = 12:06

La durata dei Crepuscoli è immediatamente ricavabile dalle tabelle in funzione della data e della Latitudine, confrontando l'Ora del Crepuscolo con l'Ora del sorgere o del tramonto corrispondente.

4.9       Variazione dell'Ora di alba e tramonto in funzione di Latitudine e data.

La variabilità dell'orario del sorgere e del tramonto del Sole è diretta conseguenza dell'inclinazione dell'asse terrestre rispetto all'orbita solare

Il 21 marzo, giorno dell'equinozio di primavera e il 23 settembre, giorno dell'equinozio d'autunno, il Sole si trova sul piano dell'Equatore ed illumina esattamente metà dell'emisfero boreale e metà dell'emisfero australe (Figura 4.27). La durata del Giorno e della Notte è uguale in tutto il mondo ed è pari a 12 ore.

In occasione degli equinozi, osservatori che si trovassero ai poli vedrebbero il sole sull'orizzonte, mentre osservatori all'Equatore vedrebbero passare il sole esattamente allo zenit.

In particolare, in occasione dell'Equinozio di Primavera, al Polo Nord si assiste al lento sorgere del Sole, mentre al Polo Sud inizia il lungo tramonto.

Durante l'estate nell'emisfero boreale, il Polo Nord è costantemente illuminato, mentre il Polo Sud resta al buio. La situazione si inverte nella stagione invernale nell'emisfero boreale, periodo durante il quale si ha una illuminazione costante al Polo Sud, ed un lungo periodo di oscurità al Polo Nord (Fig.4.28).

Si parla di "Sole di mezzanotte" nelle zone polari (Figura 4.29), proprio riferendosi al fatto che il Sole è costantemente sopra l'orizzonte, anche quando gli orologi segnano mezzanotte.

All'Equatore la durata del giorno e della notte è costante durante tutto l'Anno e non subisce variazioni stagionali.

Alle latitudini intermedie le variazioni di durata del giorno e della notte aumentano con la Latitudine: vicino all'Equatore queste saranno piccole; a latitudini elevate saranno molto grandi, avendo in estate notti cortissime e giorni lunghissimi, mentre in inverno si avranno solo poche ore di luce.

Si arriva ad avere ai poli sei mesi di giorno e sei mesi di notte.

Nella Figura 4.30 sono indicate le attuali posizioni degli equinozi e dei solstizi; le stagioni sono riferite all'emisfero boreale.

A causa dell'ellitticità dell'orbita la durata delle quattro stagioni non è uguale per tutte.

Le stagioni, definite come i periodi di tempo compresi tra un equinozio e il solstizio successivo, o tra un solstizio e l'equinozio successivo, hanno la durata indicata qui di seguito:

I due tropici e i due circoli polari rivestono un'importanza particolare per le condizioni di illuminazione e di inclinazione dei raggi solari nel corso dell'Anno.

Essi dividono la superficie terrestre in cinque parti caratterizzate da condizioni diverse di riscaldamento, chiamate zone astronomiche (Figura 4.31).

Esse sono: la Zona Torrida o Intertropicale, limitata dai due tropici e divisa in due dall'Equatore; la Zona Temperata Boreale, compresa fra il Tropico del Cancro ed il Circolo Polare Artico, e la Zona Temperata Australe tra il Tropico del Capricorno ed il Circolo Polare Antartico; la Calotta Polare Artica che si estende dal Circolo Polare Artico al Polo Nord e la Calotta Polare Antartica dal Circolo Polare Antartico al Polo Sud.

Nella Zona Torrida il Sole passa allo zenit di tutti i punti due volte all'Anno: all'Equatore nei giorni degli Equinozi e sugli altri Paralleli in giorni diversi; ai tropici il Sole è allo zenit una sola volta all'Anno: nel giorno del solstizio di giugno al tropico del Cancro, in quello del solstizio di dicembre al Tropico del Capricorno. Mentre all'Equatore il Giorno e la notte hanno sempre la stessa durata, negli altri punti della zona torrida si ha una differenza che però non e mai molto forte: ai tropici il Giorno più lungo è di 13 ore e 3/4, e la notte più breve è di 10 ore e 1/4. Ne deriva che in queste zone il riscaldamento è sempre molto forte e non si può parlare di vere e proprie stagioni.

Nelle Zone Temperate il Sole non passa mai allo zenit e i suoi raggi arrivano più o meno obliqui, secondo il periodo dell'Anno e la Latitudine. A parte i giorni degli equinozi, in cui dì e notte hanno la stessa lunghezza, le durate del Giorno e della notte presentano differenze che vanno aumentando con la Latitudine e con l'avvicinarsi dei giorni solstiziali; tanto che sui circoli polari il Giorno e la Notte più lunghi raggiungono, alternativamente, la durata di 48 ore perché al periodo di illuminazione (o di oscurità) del Giorno dei solstizi si collega quello di illuminazione (o di oscurità) del Giorno seguente. Nelle zone temperate, quindi, il riscaldamento varia durante l'Anno e si ha una distinzione netta tra le varie stagioni.

Nelle zone polari i raggi del Sole arrivano sempre molto obliqui e addirittura non colpiscono affatto la superficie per un periodo tanto più lungo quanto più ci si avvicina ai poli. Dopo l'equinozio di primavera nella calotta artica inizia un periodo di illuminazione che è detto gran dì, mentre nella calotta antartica inizia la grande notte; il contrario si ha invece dopo l'equinozio d'autunno.

Il gran dì e la grande notte, che vicino ai circoli polari durano pochi giorni, ai poli dovrebbero durare 6 mesi ciascuno, ma la presenza di lunghi Crepuscoli (dovuti ai fenomeni di diffusione e rifrazione della luce negli alti strati dell'atmosfera), il fenomeno delle aurore polari (legato a eruzioni nella cromosfera solare) e la stessa luminosità della Luna, accorciano sensibilmente il periodo di oscurità completa, cosicché la durata della grande notte si aggira intorno ai l00 giorni.

La suddivisione schematica in zone astronomiche, non corrisponde esattamente alla distribuzione reale delle temperature dell'aria, poiché non tiene conto dell'altitudine, dell'esposizione, della presenza di terre emerse e oceani, e di tanti altri fattori che fanno variare le condizioni termiche dei vari luoghi delta Terra producendo degli scostamenti da questo schema.

4.10    Il Calendario Giuliano e la Riforma Gregoriana.

L'Anno tropico o solare, è definito come il Tempo che intercorre tra due passaggi successivi del Sole allo zenit allo stesso tropico, cioè fra due solstizi dello stesso nome. La sua durata è di 365 giorni, 5 ore, 48 minuti e 46 secondi, ed è circa di 20 minuti più corto dell'Anno sidereo a causa della Precessione degli equinozi.

L'Anno sidereo, infatti, corrisponde al periodo della rivoluzione terrestre, ovvero all'intervallo di Tempo che passa fra due ritorni consecutivi del Sole nella stessa posizione tra le stelle, ed ha una durata di 365 giorni, 6 ore, 9 minuti e 10 secondi.

Generalmente quando si usa la parola Anno ci si riferisce all'Anno tropico o solare, poiché esso indica il periodico susseguirsi delle stagioni a cui sono collegati molti dei fenomeni fisici e biologici che si svolgono sulla Terra, comprese le attività umane.

Però nella pratica comune non è possibile utilizzare l'Anno tropico con la sua durata effettiva, dato che essa non corrisponde ad un numero intero di giorni; per ovviare a questo inconveniente si è resa necessaria l'adozione dell'Anno civile, formato da un numero non frazionario di giorni.

La differenza tra l'Anno tropico e l'Anno civile è all'origine di tutte le difficoltà insite nella elaborazione di un Calendario esatto; essa rappresenta la ragione principale della impossibilità di stabilire un Calendario perfetto, che non si trovi in errore neppure di un solo Giorno rispetto alle varie posizioni assunte dalla Terra nel suo moto di rivoluzione intorno alla Terra.

Nel Calendario usato dai romani fino ai tempi di Giulio Cesare, l'Anno veniva diviso in 12 mesi lunari e la sua durata era di 355 giorni; in tal modo esso veniva a trovarsi indietro di circa 11 giorni rispetto all'Anno solare e perciò ogni due anni si aggiungeva un mese intercalare di 22 giorni. Ma anche con questo espediente, la durata dell'Anno non risultava esatta, e pertanto con l'andare dei secoli, si arrivò ad un grave disaccordo fra le date del Calendario e le vicende stagionali, per cui si rese necessaria una correzione.

Nel 45 AC. Giulio Cesare introdusse un nuovo Calendario, che poi fu chiamato Giuliano, in suo onore.

La durata dell'Anno solare era considerata di 365 giorni e 6 ore, quindi l'Anno civile venne fissato in 365 giorni, stabilendo però di aggiungere un Giorno ogni 4 anni, in modo da compensare la differenza di 6 ore in meno rispetto all'Anno solare: dopo tre anni comuni di 365 giorni si aveva un Anno bisestile di 366 giorni, attribuendo un Giorno in più al mese di Febbraio.

Il valore dell'Anno solare adottato nel Calendario Giuliano era leggermente superiore al vero e la differenza (11 minuti e 14 secondi) si fece sentire con il passare dei secoli: verso la metà del XVI secolo la data dell'equinozio di primavera cadeva l'11 marzo invece del 21 marzo. Questo forte divario suscitò in Gregorio XIII, papa dal 1572 al 1585, una particolare preoccupazione: a lungo andare, se fosse rimasto in uso il Calendario Giuliano, la Pasqua avrebbe finito coll'essere celebrata in estate. Per evitare questo inconveniente il papa convocò una apposita commissione, costituita da illustri astronomi, matematici ed ecclesiastici, a cui affidò il compito della riforma del Calendario Giuliano. La soluzione fu trovata da Luigi Giglio, medico calabrese, il quale ideò un ingegnoso progetto di riforma che venne introdotto nel 1582 con una sola piccola modifica di Cristoforo Clavio, astronomo tedesco.

Innanzitutto si provvide ad eliminare i 10 giorni di differenza che si avevano tra Anno civile e Anno solare, e così dal 4 ottobre si passò direttamente al 15 ottobre 1582. Inoltre per evitare il ripetersi dell'errore fu stabilito che fra gli anni secolari fossero considerati bisestili solo quelli in cui il gruppo di cifre precedenti i due zeri è divisibile per 4: così mentre è stato bisestile il 1600 e lo sarà anche il 2000 non sono stati bisestili il 1700, il 1800 e il 1900.

Il Calendario Gregoriano, oltre ad essere diviso in mesi, si compone di settimane che hanno durata quasi uguale alle fasi lunari; esso conta gli anni a partire dalla nascita di Cristo.

Il Calendario Gregoriano così strutturato andrà bene fino ad oltre il 4000, poi sarà necessario togliere un ulteriore giorno ogni 30 secoli circa.

4.11    Le effemeridi aeronautiche e nautiche.

Le effemeridi sono tavole ove sono riportati, ad intervalli regolari di Tempo, gli elementi variabili dei vari astri a cui si riferiscono, relativamente all'Anno preso in considerazione.

Vi è riportato il Tempo sidereo, le coordinate di Sole, Luna, Venere, Marte, Giove, Saturno e delle principali stelle, dati sulle eclissi, carte del cielo, e una serie di tavole con le varie correzioni da apportare alle letture delle altezze di Sole, di stelle e pianeti, per tener conto dell'elevazione dell'osservatore, della rifrazione dei raggi luminosi, del diametro del Sole e della Luna, ecc. ( Figura 4.32).