Capitolo 13 - Regolo di navigazione Jeppesen

13.1    Generalità sul regolo di Navigazione

Il regolo Jeppesen, è un comodo e pratico strumento che ci permette di risolvere la stragrande maggioranza dei problemi che hanno a che fare con la Navigazione aerea, in maniera veloce e sufficientemente precisa. Tra le sue qualità più apprezzabili occorre ricordare che il regolo non ha bisogno di alcuna fonte di energia per funzionare, al contrario dei calcolatori tascabili, e quindi non c'è il rischio di trovarsi con le batterie esaurite proprio nel momento in cui si ha bisogno di effettuare dei calcoli. Inoltre, una volta impostato il regolo, è possibile effettuare una serie di calcoli in un Tempo decisamente ridotto, senz'altro più breve di quello richiesto da una calcolatrice in cui è necessario impostare ogni volta tutti i valori numerici esponendosi inoltre al rischio di errori grossolani conseguenti ad una digitazione errata.

Vi sono numerosi modelli di regoli calcolatori; quello utilizzato più comunemente è il modello CR-3 della Jeppesen; questo ha due facce, una utilizzata per i calcoli matematici e l'altra per quelli trigonometrici e geometrici.

E’ di forma circolare; in particolare la faccia per i calcoli matematici è formata da due dischi concentrici graduati esternamente in base ad una scala logaritmica; questa consente di risolvere equazioni di 1° grado, proporzioni tra i numeri e trasformazioni di unità di misura.

Per alcuni problemi specifici si usano particolari scale interne che mettono in evidenza i parametri specifici.

Coassialmente ai due dischi e superiormente a questi è montato un cursore girevole, con linea di fede centrale.

La faccia relativa ai calcoli trigonometrici si compone di tre dischi sovrapposti; quello esterno è graduato alla sua estremità con scala logaritmica.

Il mediano, è graduato alla sua estremità con due scale che partono dallo stesso punto (indice TAS) in senso orario ed antiorario, e rappresentano i valori angolari rispettivamente delle funzioni seno e coseno.

Al suo interno è presente una scala circolare degli angoli da 0° a 360° in senso orario, con al posto dello zero l'indice TC (True Course).

Inoltre, dal centro del regolo, si diramano secondo le direzioni cardinali quattro identiche scale doppie, perpendicolari tra loro, usate per la misurazione delle componenti trasversali e longitudinali del vento.

La zona all'interno della scala graduata è grigliata per facilitare le operazioni geometriche.

Vi é un terzo disco, l'interno, che ruota come gli altri intorno allo stesso asse.

Esso è trasparente, ed è graduato all'estremità con una scala da 0° a 360°. I valori sono congiunti radialmente con il centro. Infine sono presenti delle circonferenze concentriche, che sono in numero pari ai valori riportati sulle scale ortogonali del secondo disco.

Mediante l'uso del secondo e terzo disco, è possibile trasformare graficamente le coordinate polari in coordinate cartesiane e viceversa.

13.2    Operazioni base di moltiplicazione e divisione

La faccia matematica del regolo (scala esterna) ci permette di risolvere proporzioni del tipo:

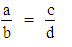
Dove "a" e "c" sono valori numerici della scala esterna, mentre "b" e "d" sono valori letti nella scala interna.

Casi particolari di proporzione sono la moltiplicazione e la divisione.

Moltiplicazione: supponiamo di voler calcolare il prodotto dei numeri "a" e "d".

Dalla relazione precedente si ha che:

a d = c b

Se sono noti "a" e "d" e si vuole conoscere il valore di "c", dato dal prodotto dei due fattori noti, basta imporre che sia "b" = 1, mantenendo l'uguaglianza.

Le scale del regolo sono graduate da 10 a 99; per noi il 10 rappresenterà l'unità.

Per effettuare la moltiplicazione imposteremo questa proporzione:

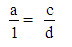
Praticamente ciò si realizza nel seguente modo:

• si pone il numero "10" della scala interna in corrispondenza di uno dei due fattori; 
• si porta la linea di fede del cursore, a sovrapporsi con il valore del moltiplicatore letto sulla scala interna;
•  si legge infine il risultato in corrispondenza della linea di fede sulla scala esterna.

Il regolo non ci permette in maniera diretta di conoscere la posizione della virgola decimale. Questa deve essere calcolata mentalmente da colui che sta effettuando l'operazione.

Per esempio una lettura di 39 può essere: 39 o 3,9 o 390 ecc.

È importante quindi che la persona che sta effettuando il calcolo abbia un'idea precisa dell'ordine di grandezza del risultato.

Il regolo infatti fornisce soltanto le cifre significative, mentre l'effettivo valore numerico deve essere determinato da colui che effettua il calcolo.

Esempio:

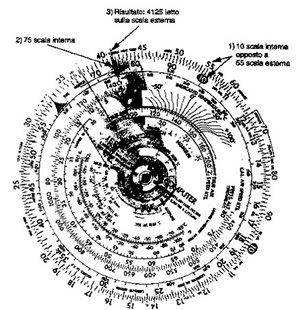
Su un aereo si sono imbarcati 55 passeggeri che pesano in media 75 Kg. Determinare il peso totale.

Ad un primo sguardo si vede che il peso sarà intorno ai 4.000 Kg.

Una volta stabilito l'ordine di grandezza del risultato si passa al calcolo con il regolo.

Si posiziona il 10 della scala interna contro il 55 della scala esterna.

Di fronte al 75 della scala interna si legge il risultato di 4.125 Kg (Figura 13.1).

La divisione può essere considerata come un caso di proporzione, e può essere risolta di conseguenza in maniera analoga alla moltiplicazione; abbiamo visto nel caso della moltiplicazione che la proporzione da impostare è la seguente:

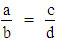
se sono noti "a" e "b" è sufficiente considerare "d" = 1 e verificare quindi la seguente uguaglianza:

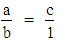
Sul regolo si posizionano dividendo e divisore in corrispondenza l'uno dell'altro. Il dividendo "a" sulla scala esterna, ed il divisore "b" sulla scala interna. In corrispondenza del numero 10 della scala interna, si legge sulla scala esterna il valore del quoziente "c".

Per quanto riguarda la posizione della virgola, ovvero l'ordine di grandezza del risultato ci si deve regolare come per la moltiplicazione.

Esempio.

Su un aereo sono stati imbarcati 20.000 Kg di combustibile che ha una densità di 0,780 Kg/litro.

Determinare il numero di litri scaricati dall'autobotte.

Dovendo effettuare una stima dell’ordine di grandezza del risultato, si vede che si dovrà ottenere un numero superiore a 20.000 e comunque dell’ordine delle decine di migliaia.

Sul regolo si posiziona quindi il numero 20 sulla scala esterna in corrispondenza del numero 78, letto sulla scala interna (per interpolazione tra il 70 e l'80).

Si legge il risultato sulla scala esterna in corrispondenza del 10 della scala interna; il numero così identificato si trova tra il 25 e il 30, ed è facile ricavare un valore pari a circa 25.640 (Figura 13.2).

Un aereo ha consumato 3.180 Kg di carburante in 37 minuti.

Calcolare il consumo orario.

Ad un primo sguardo si vede che il risultato sarà intorno ai 5-6.000 Kg/ora.

Si imposta ora la proporzione sul regolo: sulla scala interna si legge 3.180 (interpolando tra il 30 e il 35); sulla scala interna si posiziona in corrispondenza il 37 (situato tra il 35 e il 40).

Sulla scala esterna, in corrispondenza del 1:00 della scala interna (indice dell'ora che si trova al posto del numero 60) si legge 51,5.

Il risultato corretto sarà quindi 5150 Kg/ora (Figura 13.3).

13.3    Calcoli per la velocità, il Tempo, la distanza

Anche i problemi che riguardano il calcolo di velocità, tempi e distanze possono essere facilmente risolti impostando delle proporzioni nella maniera precedentemente illustrata.

Il regolo ha nel disco interno un indice chiamato "Speed Index" in corrispondenza del numero 60, e marcato 1:00.

Questo indice rappresenta i 60 minuti di un'ora e non deve essere confuso con l'indice dell'unità indicato con il numero 10.

Nel disco superiore, all'interno della scala numerica vi è una seconda scala: è quella dei tempi. In corrispondenza dello Speed Index e sotto di esso vi è 10:00, che indica un Tempo di 10 ore; sotto al numero 90 troviamo 1:30, infatti 90 minuti corrispondono a un'ora e mezzo; ancora più sotto troviamo 15:00; 900 minuti corrispondono infatti a 15 ore. È possibile procedere analogamente per tutti gli altri valori del disco interno.

Questi problemi vengono risolti facendo corrispondere la quantità considerata al Tempo impiegato (la quantità in esame deve essere letta su disco esterno e il Tempo su quello interno); in corrispondenza dello speed index è poi possibile leggere direttamente il valore orario della quantità in esame.

Esempio.

Un aereo vola con una ground speed pari a 300 Kts.

Calcolare la distanza percorsa in 40 minuti.

Dati:

GS = 300 ovvero 300 miglia in 60 minuti

Time = 40

Determinare la distanza.

Per prima cosa occorre mettere lo Speed Index sotto la GS (300).

Si legge quindi la distanza percorsa sopra il Tempo (40).

Poiché le velocità sono espresse in nodi, le distanze rilevate saranno in miglia nautiche.

La distanza percorsa è di 200 miglia (Figura 13.4).

Esempio.

Dati:

GS = 113 Kts

Distanza = 180 NM

Determinare il Tempo per percorrere la distanza indicata.

Posizionare lo Speed Index sotto la GS (113 Kts), e leggere il Tempo sotto la distanza (180 NM).

La risposta è 95.5 minuti, ovvero 1 ora, 35 minuti, 30 secondi (Figura 13.5).

Esempio.

Dati:

Distanza = 264 NM

Tempo impiegato per percorrere la distanza indicata = 1 ora 25 minuti (85 minuti)

Determinare : GS

Si posiziona il Tempo (85 minuti) sotto la distanza (264 NM) e si legge la velocità sopra lo Speed Index.

La risposta corretta è 186 Kts (Figura 13.6)

13.4    Calcoli per il consumo di carburante

I problemi che riguardano il consumo del carburante si risolvono esattamente allo stesso modo dei problemi su velocità, Tempo e distanza considerando che in questo caso alla velocità va sostituito il fuel flow ed alla distanza la quantità di carburante.

Esempio.

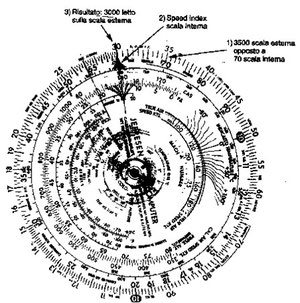
Fuel = 3.500 Kg

Tempo = 1 ora 10 minuti ( 70 minuti)

Determinare il Fuel Flow.

Posizionare il Tempo (70 minuti) sotto il fuel (3.500 Kg).

Leggere il fuel flow in KG/h sulla scala esterna in corrispondenza dello Speed Index.

La risposta in questo caso è 3.000 Kg/h (Figura 13.7).

13.5    Conversioni

Se abbiamo una grandezza espressa in un'unità di misura del sistema metrico decimale e vogliamo convertirla nel sistema anglosassone (o viceversa) è necessario conoscere i rapporti di conversione; questi sono numeri spesso difficili da ricordare. Con il regolo, invece la trasformazione di unità di misura è veloce ed immediata, senza la necessità di ricordare se non la grandezza approssimativa delle grandezze coinvolte, al fine di poter stabilire la posizione della virgola decimale dopo la trasformazione: in particolare occorre ricordare che:

Ogni unità di misura, sul regolo ha il suo indice di riferimento; nella tabellina che segue viene indicato come trovare i vari indici.

Per convertire tra due unità di misura differenti è sufficiente far corrispondere le frecce indicative delle rispettive unità di misura sulle scale esterna e interna. È possibile a questo punto leggere direttamente i valori corrispondenti sulle due scale. Il metodo è molto utile soprattutto se occorre effettuare una serie di trasformazioni, infatti una volta posizionati i due indici corrispondenti è immediato leggere i valori da determinare.

Esempio:

Trasformare 50 miglia nautiche in miglia statutarie (Figura 13.8).

Si fa coincidere la freccia delle miglia nautiche sulla scala esterna con la freccia delle miglia statutarie sulla scala interna: in corrispondenza del 50 letto sulla scala esterna si legge il valore cercato di circa 57,5 sulla scala interna.

Analogamente, ad ogni valore in miglia nautiche letto sulla scala esterna corrisponde il valore sulla scala interna espresso in miglia nautiche.

Per trasformare da miglia nautiche a Km è sufficiente far corrispondere la freccia delle miglia nautiche con quella dei Kilometri; è immediata la lettura dei valori corrispondenti sulle due scale.

Si procede in modo analogo per tutte le altre conversioni, eccetto quella tra gradi Celsius e Fahrenheit. Per queste conversioni vi è un'apposita scala a lettura diretta situata più internamente sul disco superiore.

13.6    Determinazione della Velocità vera all'aria

La velocità dell'aeromobile viene indicata correttamente dagli strumenti di bordo soltanto quando questo vola al livello del mare in atmosfera standard, e a basse velocità, tali da rendere trascurabili i fenomeni legati alla compressibilità dell'aria. Dato che queste condizioni sono incontrate soltanto occasionalmente in volo, è necessario apportare tutte le correzioni necessarie per determinare la Velocità vera all'aria o TAS.

I parametri che devono essere conosciuti sono i seguenti: 

•     la CAS (Calibrated Air Speed), ovvero la IAS corretta per la posizione dei sensori e per gli errori strumentali. Sui moderni aerei dotati di CADC (Central Air Data Computer) i dati forniti dagli strumenti sono già corretti per tutti questi errori, e quindi si legge direttamente un valore che può essere considerato la CAS; in caso contrario questa deve essere ricavata da apposite tabelle, specifiche per ogni tipo di aereo.
•     la Pressure Altitude, ossia l'altitudine letta sull'altimetro quando lo strumento è regolato su una pressione di riferimento pari a 29,92 inch/hg o 1013,2 hpa.
•     la Temperatura, che deve essere espressa in gradi centigradi.

La temperatura indicata dallo strumento di bordo è sempre superiore a quella effettiva dell'aria; questa verrebbe misurata correttamente da un termometro immobile come quello situato su un pallone sonda. Un aereo che si muove ad alta velocità provoca infatti una compressione dell'aria davanti a sé, e un conseguente aumento della temperatura per compressione adiabatica.

Il coefficiente Ct, varia con il tipo di installazione ed il disegno del sensore per ogni singolo aereo; una volta che questo coefficiente è stato individuato, non varia di molto con la quota o la velocità. Il cursore mobile del computer è marcato con una linea retta che rappresenta un coefficiente Ct pari a 0,8; vi sono poi due linee curve per il coefficiente 1,0. La linea continua è valida per la temperatura standard della tropopausa di -55°C corrispondente ad una quota di 35.000 piedi. La linea tratteggiata è invece valida per il livello del mare e una temperatura standard di 15°C. Per quote intermedie occorre interpolare tra le due linee.

Vi sono fondamentalmente due sistemi per calcolare la TAS. Il primo è quello che si adopera in pianificazione.

In questo caso i dati disponibili saranno:

• velocità indicata o numero di Mach che si vorrà mantenere in crociera; questo parametro è funzione delle prestazioni dell'aereo
• livello di volo prescelto (corrispondente alla pressure altitude)
• temperatura vera dell'aria (TAT = True Air Temperature) al livello di volo considerato (dato che si ricava dalle Carte meteorologiche)

Per aerei che volano a velocità tali da poter trascurare gli effetti della compressibilità dell'aria il metodo consiste nel far corrispondere la pressure altitude con la temperatura vera dell'aria nella finestra indicata con "True Air Speed" e "Density Altitude". Il valore di TAS viene quindi letto sulla scala esterna in corrispondenza del valore di CAS sulla scala del disco mobile.

Esempio.

TAT = - 10°C

PA = 7.000 ft

CAS = 110 Kts

determinare : TAS e density altitude

Per prima cosa posizionare la TAT in coincidenza con la PA nella casella piccola interna denominata "True Air Speed".

Passando adesso alle due scale esterne del regolo, è possibile leggere in corrispondenza della CAS (scala interna) il valore della TAS (scala esterna).

La risposta esatta è: TAS = 119,5 Kts che arrotonderemo a 120 Kts

La density altitude si legge nella finestra interna della casella della "True Air Speed" mostrata nella Figura 13.9. Il suo valore è di 5000 ft.

Esempio.

CAS = 200 Kts

PA = 8000 Ft

TAT = 0°C

Calcolare la TAS

Mediante il sistema sopra esposto si ricava che la TAS è 226 nodi (Figura 13.10).

A velocità elevate gli effetti di compressibilità diventano non più trascurabili, ed anzi ad un certo punto diventano di importanza primaria per la condotta dell'aereo. Bisogna quindi fare riferimento al numero di Mach. Il metodo per il calcolo della TAS in questi casi, viene spiegato nell'esempio seguente, riferito anch’esso alla fase di pianificazione del volo.

Esempio.

Mach = 0,75

TAT = -50°C

Determinare la TAS.

Ruotando il disco superiore, osservando la casella della Press. Alt. nella finestra denominata True Air Speed, oltre il fondo della scala, è possibile individuare una doppia freccia con indicazione Mach index.

Se si porta questo indice in corrispondenza della TAT (True Air Temperature) è possibile trovare la TAS (435 Kts) sulla scala esterna del regolo in corrispondenza del numero di Mach (75) letto sulla scala interna Figura 13.11).

Il secondo metodo di calcolo della TAS è applicabile in sede di effettuazione del volo, quando sarnno conosciuti:

•  velocità indicata (IAS) o numero di Mach
•  livello di volo e corrispondente pressure altitude
•  temperatura indicata dell'aria (RAT = Ram Air Temperature)
•  Ct, che viene sempre considerato 1.0 tranne quando diversamente indicato.

Si posiziona la CAS in corrispondenza della PA. Si muove poi il cursore mobile fino a quando la linea curva del coefficiente Ct interseca la linea a spirale.

Si legge quindi, nella finestra sottostante, la TAS ed il numero di Mach. Si può anche ricavare il Temperature Raise, che permette di ricavare la TAT per differenza.

Esempio:

CAS : 300 Kts

PA = 20.000 ft

RAT = -10°C

Determinare : Mach, Raise, TAS.

Si ricerca il valore della CAS nella finestra relativa e lo si porta a coincidere con il valore della PA.

Mantenendo il regolo in questa posizione si fa scorrere il cursore in modo che la curva per Ct = 1.0 si sovrapponga all'intersezione della linea di RAT con la curva a spirale.

La linea di fede del cursore indicherà una TAS pari a 395 nodi, un numero di Mach di 0,65 e un temperature raise di 20°C (Figura 13.12).

13.7    Risoluzione del Triangolo del vento con il regolo Jeppesen

Sul retro del regolo vi sono tre dischi concentrici che permettono la risoluzione di un Triangolo del vento.

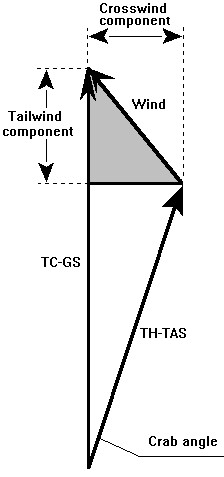
Questo è già stato esaminato in precedenza dal punto di vista grafico; rivediamo brevemente i suoi componenti (Figura 13.13):

Se nel Triangolo del vento sopra indicato tracciamo una linea passante per il vertice del vettore proprio e perpendicolare alla Rotta vera, possiamo identificare le due componenti del vento: crosswind e headwind o tailwind (Figura 13.14).

Il triangolino evidenziato è quello che viene riportato sul regolo (Figura 13.15).

Si assume, in questo tipo di diagramma, che sia possibile sommare la componente lungo la direzione della Rotta (headwind o tailwind) alla TAS. Questo è possibile, commettendo un errore trascurabile, fino a quando l'angolo di Crab è inferiore ai 10°. Per angoli superiori è necessario apportare delle correzioni di cui parleremo in seguito.

Questo Triangolo può essere risolto sul regolo senza tracciare tutti i vettori, ma limitandosi a tracciare un puntino con la matita sul disco trasparente, punto che rappresenta la coda del vettore vento, essendo il suo vertice situato al centro del regolo. Il puntino a matita può essere poi cancellato facilmente passandoci sopra con un dito.

Esempio 1.

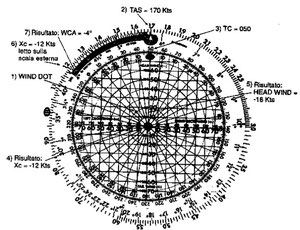
TC = 050°

TAS = 170 Kts

W = 010° / 20 Kts

Determinare : TH, GS, WCA.

Per prima cosa occorre marcare con la matita l'intersezione della linea che indica la direzione di provenienza del vento (010°) con la circonferenza di raggio pari alla velocità del vento sul disco trasparente (WIND DOT).

Poi si deve ruotare il disco intermedio fino a che sull'indice TAS corrisponda sul disco esterno il valore della TAS (170 Kts).

Il disco trasparente deve essere ruotato fino a che il valore della TC (050°) si venga a trovare sopra il TC index.

Una volta effettuate queste due rotazioni, il regolo sarà pronto per la risoluzione del problema.

Proiettando il punto marcato a matita sulla scala orizzontale si otterrà la componente trasversale del vento (Xc = -12 Kts). Il valore sarà negativo come evidenziato sul regolo (left crosswind -).

Il valore numerico di componente trasversale del Vento deve essere letto ora sulla scala esterna del regolo. Approssimativamente in corrispondenza di questo valore, sulla scala intermedia, leggeremo il WCA (-4°) che avrà segno concorde con la componente del vento al traverso (Figura 13.16).

Con il valore del WCA si ricava la TH:

TH = TC + WCA

con il WCA di segno positivo o negativo a seconda che l'angolo sia a destra o a sinistra.

In caso di angoli di WCA maggiori di 10° occorre leggere, sul disco intermedio in senso antiorario sulla scala nera, il valore di WCA trovato ed in corrispondenza di esso sulla scala esterna leggere l'ETAS.

A questo punto proiettando il punto marcato a matita sulla scala verticale si legge la componente longitudinale del vento (Wc = -16 Kts), che assumerà in questo caso valore negativo come evidenziato sul regolo (headwind -).

La GS viene calcolata mediante la formula:

GS = ETAS + Wc

ETAS = TAS per Crab angles < 10°

Esempio 2.

TH = 050°

TAS = 110 Kts

W = 090° / 20 Kts

Determinare: TC, GS

Per risolvere questo genere di problema del vento è necessario posizionare la TC e la TAS in corrispondenza dei rispettivi indici sul regolo.

Siccome la TC, in questo problema, non è un dato noto, posizioniamo temporaneamente l'indice TC sotto la TH per ottenere una Xc approssimata (Figura 13.17).

Con questo valore si determina un WCA approssimato che sottratto alla TH ci dà una TC approssimata.

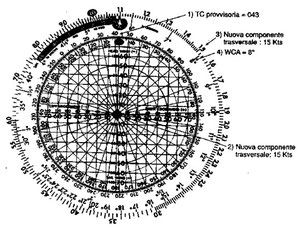
Con la nuova TC si ripete la procedura appena descritta per ricavare un nuovo WCA che sottratto alla TH ci dà una nuova TC (Figura 13.18).

Si prosegue in questo modo fino a quando non si ottiene un WCA uguale a quello precedente; questo valore di WCA determinerà la TC reale (Figura 13.19).

Il calcolo della GS viene effettuato come nel primo problema.

Esempio di schema di calcolo con risultati:

Wc = -13 Kts ETAS = 109°             GS = 96 Kts

Nelle figure seguenti sono evidenziati i passaggi.

Abbiamo detto precedentemente che tutti i problemi del vento presentano sei variabili e, date quattro di esse, possono essere ricavate le altre due.

Per trovare il vento in volo tutti i dati devono essere noti eccetto la velocità del vento e la sua provenienza.

Si dovranno posizionare la TC e la TAS in corrispondenza dei propri indici; poi, dopo aver trovato le due componenti del vento è cosa semplice trovare le coordinate di cui abbiamo bisogno per marcare il vento sul regolo.

Esempio 3.

TC = 216°

TAS = 150 Kts

TH = 220°

GS = 130 Kts

Determinare: W

Si inizia posizionando la TAS (150 Kts) in corrispondenza del TAS index e la TC (216°) sotto il relativo indice.

Si esegue poi l'operazione TH - TC = WCA (220° - 216° = +4°).

Si vede in corrispondenza del WCA (+4°) sulla scala bianca intermedia il valore di Xc (+10°). Questo avrà il medesimo segno del WCA.

Si determina quindi il valore dell'ETAS come da primo esempio: in questo caso ETAS = TAS

Si esegue infine il calcolo:

GS - ETAS = Wc       (130 - 150 = - 20 Kts).

Si marca il vento operando sul regolo come per una coppia di assi cartesiani; si individua così un punto utilizzando come coordinate Xc e Wc (Figura 13.20).