Capitolo 10 - Cenni di Teoria degli Errori

10.1    Analisi degli errori, studio e calcolo dell'incertezza nella misura

 

L'esperienza ha mostrato che nessuna misura, per quanto fatta con cura, può essere completamente libera da errori. La Navigazione, sia essa stimata o strumentale, dipende da una serie di misure di vari parametri, ed ha quale risultato la determinazione della posizione, ovvero il calcolo di un dato numerico, che può esplicitarsi come una coppia di coordinate, Latitudine e Longitudine, o come un Rilevamento ed una distanza da un punto conosciuto. È perciò della massima importanza essere in grado di calcolare gli errori e di ridurli per quanto possibile al minimo.

 

Nella scienza la parola "Errore" non implica il solito significato di "sbaglio" o "svista". "Errore" in una misura significa l'inevitabile incertezza che è presente in tutte le misure. Come tali gli errori non sono sbagli; non si possono evitare neanche operando con molta cura. Il meglio che si può fare è di assicurarsi che questi siano il più ragionevolmente piccoli possibile, e di avere qualche stima realistica di quanto essi sono grandi.

 

Per quanto riguarda la lettura degli strumenti, per esempio, l'Errore è tra l'altro funzione del tipo di scala graduata che viene usata: dovendo per esempio valutare la posizione di una lancetta rispetto ad una scala graduata presa quale riferimento, nel caso in cui la lancetta non si trovi esattamente in corrispondenza di una delle divisioni, occorre effettuare una interpolazione, che è una tecnica che porta a risultati inevitabilmente approssimati, ossia affetti da un certo Errore.

La bontà della lettura può chiaramente dipendere anche dalla distanza, posizione, grandezza, angolazione, illuminazione e vibrazioni dello strumento. Gli strumenti elettronici su aerei con glass-cockpit, nei quali si ha sia l'indicazione analogica che il valore digitale chiaramente rappresentato, permettono di ridurre grandemente questo tipo di Errore di lettura.

 

Molte misure implicano errori che sono molto più difficili da stimare di quelli connessi con il localizzare un punto su una scala. Per esempio, quando misuriamo un intervallo di Tempo utilizzando un cronometro, la principale sorgente di Errore non è la difficoltà di leggere il quadrante, ma il nostro Tempo di reazione incognito nel far partire e nel fermare l'orologio. Questo genere di incertezze possono talvolta essere stimate ragionevolmente, se possiamo ripetere la misura parecchie volte. In questi casi, lo sparpagliamento dei nostri valori ci dà una indicazione preziosa dell'Errore nelle nostre misure.

 

Non sempre si può fare assegnamento su misure ripetute per rivelare gli errori. In particolare, su un aereo, ogni misurazione, (sia essa di velocità o di scarto radio o di qualsivoglia parametro), è in un certo senso sempre unica, in quanto le condizioni complessive sono costantemente mutevoli.

 

10.2    Valore medio

 

Il valore medio è la migliore stima della grandezza considerata, a seguito di una serie di misure.

In presenza di sorgenti di incertezza casuali, dopo aver identificato tutte le sorgenti di Errore sistematico e di averle ridotte ad un livello trascurabile, si procede ad una serie di misurazioni della grandezza considerata. La media è data dalla somma dei valori trovati diviso per il loro numero.

 

xmed = (x1 + x2 + ...+ xn) / n

 

ovvero, con simbolismo più rigoroso:

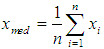
Esempio:

Con un metro a nastro si vuole determinare la lunghezza di una stanza. La misura viene ripetuta tre volte, ottenendo i seguenti valori: 4,53 m, 4,50 m, 4,51 m.

Il valore esatto della lunghezza che vogliamo determinare, non è conosciuto, come del resto dimostrato dal fatto che in tre misurazioni abbiamo ottenuto tre risultati diversi: la migliore stima della misura è però data dal loro valore medio che è così ricavabile:

Lmed = (4,53+4,50+4,51) : 3 = 4,51 m

 

10.3    Deviazione standard

 

La deviazione standard (s) è una stima della incertezza media delle misure x1, x2,...,xn. Questa è un numero caratteristico che discende dalla distribuzione dei valori misurati della grandezza esaminata. La formula per ricavare questo numero è abbastanza complicata, ma molti calcolatori tascabili, oggi sono in grado di fornirla con rapidità ed immediatezza.

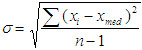
Se le misure si distribuiscono normalmente intorno al valore medio, secondo una curva di distribuzione di Gauss, il 68% circa dei valori si troveranno in un intervallo situato a cavallo del valore medio, e di ampiezza pari a una distribuzione standard sopra e sotto al valore medio: (Xmed-s Xmed +s) (Figura 10.1).

La percentuale sale al 95% se si considera un intervallo pari a due deviazioni standard sopra e sotto il valore medio.

Si sale al 99% nel caso di 3s.

Un valore piccolo di s indica che le misure sono tutte molto vicine al valore medio, e che quindi la curva di distribuzione è alta e stretta. Grandi valori di s, al contrario indicano la presenza di notevoli errori casuali e la distribuzione dei valori misurati in un ampio intervallo. A questo caso corrisponde una curva di distribuzione larga e bassa.

   

10.4    Grandezze derivate

 

La maggior parte delle grandezze fisiche non possono di solito essere misurate con una singola misura diretta, ma vengono invece determinate in due passi distinti. In primo luogo, occorre misurare le grandezze x, y, che possono essere misurate direttamente e dalle quali la grandezza che ci interessa può essere ricavata. In secondo luogo, utilizzando i valori misurati di x e y, si calcola la grandezza in questione. Per esempio, per trovare l'area di un rettangolo, si misurano la sua lunghezza l e la sua altezza h, e quindi si calcola la sua area A come A = lh. Analogamente, il modo più ovvio per trovare la velocità v è quello di misurare la distanza percorsa d, il Tempo impiegato, t, e quindi di calcolare v come:

 

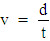
Quando una misura comporta questi due passi, anche la stima dell'Errore necessita di due passi. Dapprima occorre stimare gli errori nelle grandezze che sono misurate direttamente, e quindi trovare come questi errori si propagano attraverso i calcoli per produrre un Errore nel risultato finale.

 

10.5    Propagazione degli errori nelle somme e nelle differenze

 

Vediamo come si propagano gli errori nel caso di somme e differenze. Si dimostra che se alcune grandezze sono misurate ognuna con una incertezza determinata, l'incertezza del risultato è pari alla somma delle incertezze degli addendi.

q = x - y + . . .- z

 

dq = dx + dy + . . .+ dz

Esempio:

Determinare l'incertezza nella somma di tre distanze, ognuna delle quali è conosciuta con la incertezza in più o in meno di un miglio.

 

AB = 100 ± 1

BC = 240 ± 1

CD = 160 ± 1

AD = 100 + 240 + 160 = 500

dAD = ± 1 ± 1 ± 1= ± 3

 

L'incertezza in più o in meno è di 3 miglia, dato dalla somma delle incertezze nella misura dei tre addendi.

 

 

10.6    Propagazione degli errori nelle moltiplicazioni e nelle divisioni

 

L'Errore percentuale di una misura è dato dalla seguente formula:

 

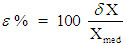
Quando si moltiplicano o si dividono delle grandezze, gli errori percentuali si sommano.

 

Esempio:

La distanza tra i punti A e B è pari a circa 200 miglia con una approssimazione di 5 miglia pari al 2,5%. La velocità mantenuta è di circa 200 Kts più o meno 10 nodi, ovvero con una approssimazione del 5%.

Calcolare il Tempo per percorrere la distanza e il suo Errore probabile.

 

Il Tempo è ottenuto dividendo la distanza per la velocità. È immediato vedere che il Tempo necessario sarà di un'ora circa.

Per quanto riguarda l'ordine di grandezza degli errori, occorre ricordare che in presenza di moltiplicazioni e divisioni, come in questo caso, si sommano gli errori percentuali, perciò:

 

e%Tempo = e%distanza + e%velocità

 

e%Tempo = 5% + 2,5% = 7,5%

 

Il 7,5% di un ora corrisponde a 4 minuti e mezzo.

Per percorrere la distanza considerata, in presenza di errori di quest'ordine di grandezza impiegheremo un Tempo compreso tra i 55,5 e i 64,5 minuti.

Nel caso di un prodotto di una grandezza misurata per un numero esatto, se la grandezza x è misurata con Errore dx ,ed è utilizzata per ricavare il prodotto q = Nx, dove N non ha Errore, allora l'Errore in Q è N volte quello in x.

 

eq = N dx

Esempio:

Determinare lo spessore di un foglio di carta utilizzando un comune righello determinando contestualmente l'errore probabile della misura.

 

Dato che la determinazione dello spessore di un singolo foglio con una certa precisione, dati i mezzi a disposizione è praticamente impossibile, prendiamo una risma di 500 fogli e misuriamo il suo spessore, che supponiamo essere di 53 mm più o meno 1 mm.

In questo caso avremo N = 1 / 500

Lo spessore di un foglio sarà: 53 / 500 = 0,106 mm

L'Errore nella misura sarà: 1 / 500 = 0,002 mm ossia due millesimi di millimetro.

 

1.7       Sbagli ed errori

 

Nella nostra lingua “errore” ha due significati: il primo legato è all’imprecisione (per esempio di una misura), e il seconda è invece inteso nel significato di sbaglio.

 

Si parla di errore di una misura quando per esempio si cerca di misurare una stanza con un metro a nastro. Probabilmente riusciremo a determinarne le dimensioni con la precisione di un centimetro, ovvero a fronte di una misura ottenuta pari per esempio a 4 metri e 51 centimetri, la stanza potrebbe essere in realtà lunga 4 metri e 52, o quatto metri e 50.

 

Spesso possiamo disinteressarci di piccoli errori, ma quando la precisione è importante siamo costretti ad adottare strumenti di misura più accurati e particolari metodologie per il loro utilizzo.

 

Parliamo invece di sbaglio quando per esempio utilizziamo un metro a nastro graduato in pollici credendo di misurare in centimetri, ottenendo quindi un valore numerico completamente errato.

 

Nelle nostre cabine di pilotaggio abbiamo moltissimi strumenti, e siamo tenuti a conoscere il livello di errore che possiamo accettare, per esempio nella lettura di un altimetro o nella misura di una tensione o di una frequenza.

 

Spesso l’errore è espresso in percentuale rispetto alla grandezza in esame; la cosa importante comunque è quella di avere una chiara idea della grandezza dell’errore accettabile, ovvero che genere di imprecisione possiamo accettare senza che questo metta a repentaglio le nostre normali operazioni.

 

Parliamo invece di sbaglio quando l’errore è grossolano, per esempio se sbagliamo l’unità di misura, pollici invece di centimetri, o aggiungiamo uno zero di troppo, o adoperiamo uno strumento non correttamente tarato.

Recentemente sono intervenuto in una conversazione abbastanza concitata tra un controllore di volo di Ciampino e un aereo americano che secondo il controllore stava volando troppo basso rispetto ai 4000 ft a cui era autorizzato. Il controllore continuava a ripetere il settaggio altimetrico di 988 (mb) mentre il Pilota aveva capito 2988 (inches of mercury). Questo è un esempio di sbaglio, che nel caso specifico faceva volare l’aereo in questione circa 800 ft sotto alla quota prevista.

 

Sia un errore fuori tolleranza che uno sbaglio possono portare a gravi conseguenze nel nostro mestiere, non per niente una delle cose più importanti è la situation awareness, ovvero la consapevolezza della situazione complessiva.

Al fine di evitare sbagli, sono poste in essere particolari procedure e metodologie di lavoro, perché quanto più grave è la conseguenza legata ad un’azione o una decisione sbagliata, tanto più attente devono essere le procedure implementate, in modo da ridurre la probabilità di un tale evento.

 

Al fine di ridurre gli “sbagli” legati in particolare al fattore umano si cerca innanzitutto di selezionare il miglior materiale umano disponibile, di prepararlo adeguatamente, controllarlo periodicamente e incentivarlo ad un miglioramento continuo.

 

Tra le metodologie di lavoro adottate, fondamentale è l’uso standardizzato di procedure guides e checklist, l’uso del read-back per le comunicazioni, il controllo incrociato, la crew coordination e integration, il crew resources management.

 

Il cervello dell’uomo è fallibile, soprattutto in situazioni di forte stress, magari unito a stanchezza. Una sequenza di azioni, se disturbata o interrotta può non essere completamente portata a termine, anche se il nostro cervello la ha già catalogata come conclusa, oppure può essere effettuata un’azione non corretta con la convinzione di stare facendo quella giusta.

Questi sono fenomeni che sicuramente molti di noi hanno avuto occasione di sperimentare sulla propria pelle anche nella vita di tutti i giorni.

 

Sugli aerei multi-crew, uno dei modi per ridurre le probabilità di errore è quello di fare le cose in due, o meglio, un Pilota le fa e un altro le verifica.

 

In alcune particolari situazioni critiche è bene che entrambi i Piloti concordino preventivamente alcuni tipi di azioni, in quanto non è concesso di sbagliare, ed è quindi bene che entrambi effettuino un doppio controllo prima della loro esecuzione.

 

A tal proposito vi sono alcune azioni particolarmente delicate da effettuare in emergenza quali lo spegnimento di un motore in volo o l’isolamento di impianti critici, e, durante le operazioni normali, manipolazioni FMS che vanno a modificare la rotta o il profilo verticale.

 

La maggior parte delle compagnie mondiali, proprio per evitare “sbagli” disastrosi, hanno adottato procedure particolarmente restrittive. Ad esempio quelle collegate allo spegnimento dei motori in volo in emerenza, non sono autorizzate senza il preventivo controllo incrociato di un altro membro di equipaggio.

 

Ricordiamo che c’è stato un famoso incidente provocato dallo spegnimento in volo dell’unico motore funzionante, e che lo stesso evento non è poi così raro al simulatore.

1.8       Feedback

 

A volte è difficile o poco agevole la determinazione esatta di alcuni parametri, per cui si preferisce procedere per tentativi successivi. Si inizia tentando con un valore ragionevolmente vicino a quello che ci si aspetta, e poi in funzione della risposta ottenuta si modifica l’input, in modo da ottenere un risultato più vicino a quello desiderato. Si procede in questo modo per esempio nei bombardamenti terrestri: osservando dove finisce il colpo si imposta la necessaria correzione per il successivo. Dopo un certo numero di tentativi si riesce a centrarlo, o ad andarci sufficientemente vicino. Si agisce in maniera analoga quando si cerca di mantenere una quota o una velocità con pilotaggio manuale. Attraverso l’osservazione degli strumenti si nota l’errore tra la prestazione ottenuta e quella attesa, si imposta quindi una correzione per riportarsi all’interno delle tolleranze ammesse, che per le velocità possono essere per esempio +10/-5 kts e per le quote +/- 100 ft.

 

Processi ad alto rischio e/o ad alto costo non permettono di arrivare ai risultati attesi per tentativi e successive approssimazioni, ma richiedono che si arrivi a quanto voluto il più direttamente possibile.

A tale fine, occorre avere mezzi adeguati, tecnicamente aggiornati e adeguatamente mantenuti in efficienza; personale adeguato, convenientemente selezionato formato e controllato; processi di feedback che si svolgano a livello individuale, strutturale e organizzativo.

Il feedback è un fattore indispensabile in quanto i processi aperti tendono ad essere instabili

 

Caratteristiche desiderabili di un processo di feedback

            |- immediatezza

            |- obiettività

            |- comprensibilità

            |- riservatezza

            |- significatività

            |- accettabilità

 

Feedback

            |- individuale

            |           |- autocritica

            |           |- critica da parte dell’altro C/M

            |           |- controlli periodici

            |           |- DFOM

            |

            |- strutturale

            |           |- digital flight data recorder analysis

            |           |- flight log

            |           |- controlli periodici

            |           |- segnalazioni personale navigante

            |           |- safety report

            |

            |- organizzativo

                        |- audit

                        |- management review